Если функция у=ƒ (х) имеет производную ƒ ¢(х), которая, вообще говоря, сама является дифференцируемой функцией, то производная от ƒ ¢(х) называется производной второго порядка (или второй производной) от функции ƒ (х) и обозначается: уи, ƒ ¢¢(х), т. е.
ƒ ¢¢(х)=(ƒ ¢(х))¢.
Аналогично, производной третьего порядка (третьей производной) от функции ƒ (х) называется производная от второй производной ƒ ¢¢(х), т. е.
ƒ ¢¢¢(х)=(ƒ ¢¢(х))¢.
Производная четвертого порядка
ƒ IV(х) = (ƒ ¢¢¢(х))¢.
Например, для функции
ƒ(х)=2 х 6–sin3 x
ƒ¢(x)=12 x 5–3 cos 3 x,
ƒ¢¢(x)=12·5 x 4–3·(– sin 3 x)·3=60 x 4+9 sin 3 x,
ƒ¢¢¢(x)=60·4 x 3+9· cos 3 x ·3=240 x 3+27 cos 3 x,
ƒIV(x)=240·3 x 2–27 sin 3 x ·3=720 x 2–81 sin 3 x и т. д.
Производную порядка n обозначают:
y(n ) или ƒ(n)(x).
Приложения дифференциального исчисления
Были рассмотрены некоторые приложения производной, а именно: задача о касательной к графику функции, отыскание интервалов монотонности функции. С помощью производных вычисляются пределы, приводящие к неопределенностям 
и 
.
Правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или двух бесконечно
больших функций равен пределу отношения их производных.
Заметим, что речь идет о дифференцируемых функциях, во-первых, и во-вторых, предел отношения производных вычисляется при том же условии, что и данный предел.
Итак,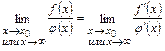 
, ес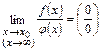ли
или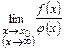 
= 
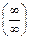
Пример 1.
Найти следующие пределы
1) 
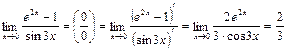
2) 
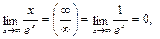т. к.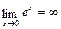 
, 
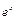– бесконечно большая при х®∞
3) 
т. к. cos 5π=cos(4π+π)=cos π= –1.
cos 3π=cos(2π+π)=cos π= –1.
Рассмотрим случай неоднократного применения правила Лопиталя.
4) 
.
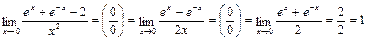Правило Лопиталя было применено дважды.
Рассмотрим случай, когда правило Лопиталя не приводит к желаемому результату.
5) 
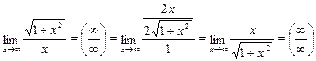
Применение правила Лопиталя не позволяет раскрыть эту неопределенность, но предел этот легко вычисляется, если числитель и знаменатель дроби одновременно разделить на х
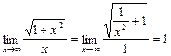, т.к. 
.
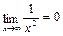Правило Лопиталя помогает раскрыть неопределенности вида 0·∞, ∞–∞.
6) 
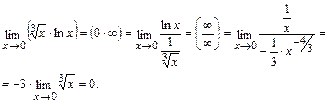
7) 
,
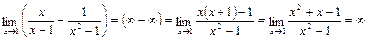т. к. 
Экстремум функции
Исследование функции на экстремум – одно из важнейших приложений производных. Рассмотрим определение минимумов и максимумов, и способы их отыскания.
Пусть функция ƒ(х) определена и дифференцируема на некотором множестве и точка х 0 – точка внутри него.
Определение. Функция ƒ (х) в точке х 0 имеет максимум (минимум), если
существует такая окрестность точки х 0, что для всех х из
этой окрестности
ƒ (х) < ƒ (х0) (ƒ (х) > ƒ (х0)).
 |
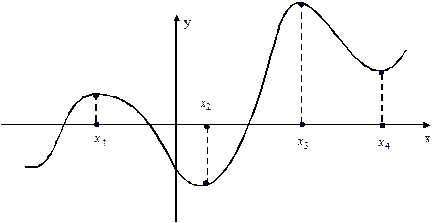Точка х 0 называется тогда точкой максимума (минимума).
Рис. 25.
Показан график функции, которая имеет две точки максимума (х 1 и х 3) и две точки минимума (х 2 и х 4), причем максимальное значение может оказаться меньше минимального (ƒ (х1) < ƒ (х 4)). Это подчеркивает тот факт, что мы характеризуем особенность функции только вблизи некоторой точки.
Значения функции в точках максимума и минимума называют экстремальными значениями или экстремумами. На приведенном графике видно, что точки экстремума (х 1, х 2, х 3, х 4) определяют интервалы монотонности функции, в каждом из которых производная сохраняет определенный знак. В точках экстремума, понятно, производная обращается в нуль. Сформулируем теорему о необходимом условии существования экстремума.
Теорема. Если функция ƒ (х) в точке х 0 имеет экстремум, то производная
функции в этой точке равна нулю, т. е. ƒ¢(х 0)=0.
Заметим сразу, что условие это не является достаточным, т. е. обратное утверждение не всегда верно. Из равенства ƒ ¢(х 0) = 0 не обязательно следует, что в точке х 0 существует экстремум.
Подтверждением тому пример с функцией ƒ (х) =х 3.
Найдем ƒ ¢(х) = 3 х 2. В точке х =0 ƒ ¢(0)=0. Но как угодно близко к точке х =0 найдем х >0, где ƒ (х) =х3 > 0, найдем х <0, где ¦(х)= х 3<0. Т. е. не существует какая-либо малая окрестность точки х =0, где для всех х значение функции в точке х =0 будет самым большим или самым малым. Поэтому точка х =0 не является точкой экстремума.
Можно рассуждать иначе. Так как производная ƒ¢(х)=3х2, то функция ƒ(х)=х3 возрастает при любых действительных х и экстремумов не имеет.
Точки, в которых выполняется необходимое условие экстремума (ƒ¢(х)=0) называются критическими.
Очевидно, что касательная к графику функции в точках, где ƒ ¢(х)=0, параллельна оси абсцисс Ох.
Достаточное условие экстремума дается в следующих теоремах.
Теорема 1. Если х 0 – критическая точка функции и при переходе через
нее производная меняет знак, то х 0 – точка экстремума, а
именно, если производная меняет знак с плюса на
минус – точка максимума, если – с минуса на плюс – точка
минимума.
Заметим, что экстремума в точке нет, если производная не меняет знака. Правило исследования на экстремум с помощью первой производной известно из школьного курса. Достаточное условие экстремума иногда удобнее формулировать с помощью второй производной.
Пусть функция ƒ(х) дважды дифференцируема в некоторой области (т. е. ƒ(х)имеет ƒ¢(х) и ƒ ¢¢(х)).
Теорема 2. Если х 0 – критическая точка функции ƒ(х) и ƒ ¢¢(х0) > 0, то
х 0 – точка минимума, если ƒ¢¢(х0) < 0, то х 0 – точка максимума.
С помощью второй производной определяется выпуклость или вогнутость графика функции.
