Бесконечно малые и бесконечно большие функции

Определение. Бесконечно малой при х ® х ₀ называется функция α (х), предел

которой при х ® х ₀ равен нулю, т. е.

Для бесконечно малых верны теоремы о пределах функций, а именно:

–сумма конечного числа бесконечно малых функций есть функция бесконечно малая;

–произведение бесконечно малых есть функция бесконечно малая;

–произведение бесконечно малой на постоянную есть функция бесконечно малая;

–произведение бесконечно малой на функцию ограниченную есть функция бесконечно малая.

Например, α ₁(х)=(х –2)² – функция бесконечно малая при х ®2.

α ₂(х)= sin x – функция бесконечно малая при х ®π.

α ₃(х)= х ²–3 х +2 – функция бесконечно малая при х ®1.

Обратимся теперь к рассмотрению функций, значения которых в окрестности точки х ₀ не ограничены.

Определение. Функция ƒ(х) называется бесконечно большой

при , если для любого положительного числа М

найдется такое положительное число δ, что для каждого х

из δ -окрестности точки х ₀ выполняется неравенство |ƒ(х)| > М.

 

Примером такой функции является функция tg х при .

Функция при х ®0 также является бесконечно большой. Если ƒ(х) – бесконечно большая при х®х₀ функция, то записывают:

 

.

Здесь знак ∞ (бесконечность) указывает, что функция не имеет предела и является бесконечно большой.

Сформулируем теорему о связи бесконечно малой и бесконечно большой функций.

Теорема. Если функция α (х) – бесконечно малая при х®х ₀, то –

бесконечно большая функция при х®х ₀.

Если ƒ(х) – бесконечно большая функция при х®х₀, то

– бесконечно малая функция при х®х₀.

Например, если sin x – бесконечно малая при х® 0, то – бесконечно большая при . Или при х ®3 функция х –3®0, а функция .

Заметим, что отношение любой функции, стремящейся к конечному пределу, и функции бесконечно малой является функцией бесконечно большой.

Поэтому, , т. к. , а .

Рассмотрим поведение функций при неограниченном возрастании аргумента х. Говорят х ®∞ (неограниченно возрастает по абсолютной величине), если для любого числа М > 0 переменная х примет значение

| х | > М

 

Можно говорить о пределе функции при х ®∞. Если при этом существует предел А функции ƒ(х), то записывают

Все рассмотренные теоремы и правила вычисления предела справедливы и в этом случае.

Например, – бесконечно малая функция при х ®∞, т. к. .

 

Непрерывность функции

Понятие непрерывности функции интуитивно связано с непрерывностью линии (графика функции). С точки зрения математика это понятие связано с существованием предела функции в точке.

Рис. 17. Рис. 18

. Рис. 19. Рис. 20.

На рисунках 17–20 представлены графики различных функций, из которых только одна (рис. 20) является непрерывной в точке х ₀. Остальные функции не являются непрерывными в точке по разным причинам. На рис. 17 дан график функции, которая имеет в точке х ₀ различные (хотя и конечные) односторонние пределы. На рис. 18 функция в точке х ₀ не имеет конечного правого предела. На рис. 19 функция имеет оба равные односторонние пределы, но сама в точке х ₀ не определена. Таким образом, для непрерывности функции в точке должны быть устранены все эти особенности.

 

Определение. Функция ƒ(х) называется непрерывной в точке х ₀, если

1) она определена в точке х ₀ и в некоторой ее окрестности,

2) существует ,

3) предел функции в точке х₀ равен значению функции в

этой точке, т. е.

Второе условие определения может быть сформулировано более подробно: существуют и равны оба односторонних предела в точке, т. е.

 

 

Рассмотрим примеры.

№ 1. .

Эта функция не является непрерывной в точке х =0, т. к. в этой точке она не определена.

 

№ 2. .

Эта функция не является непрерывной в точке х =2, т. к. в этой точке не существует ее предел: .

Заметим, что в точке х =2 тоже не определена.

 

№ 3. Зададим функцию с помощью двух аналитических выражений, а именно

 

 

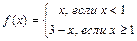
Посмотрим, является ли эта функция непрерывной в точке х =1. Значение функции в этой точке ƒ(1)=3–1=2. Функция определена для всех действительных чисел.

Вычислим односторонние пределы. При х < 1 ƒ(х)=х, поэтому

 

 

При х > 1 ƒ(х)=3– х, поэтому

 

 

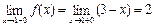
Так как односторонние пределы не равны между собой, то не существует и в точке х =1 функция не может быть непрерывной.

Определение. Функция называется непрерывной на отрезке, если она

непрерывна в каждой точке этого отрезка.

 

Рассматривая простейшие элементарные функции, легко убедится, что каждая из них непрерывна в области своего определения.

Определение. Точка х=х₀ называется точкой разрыва функции, если в

этой точке нарушается хотя бы одно требование

непрерывности.

 

На рисунках 17–19 приведены примеры точек разрыва.

Точку называют точкой разрыва первого рода, если существуют и конечны оба односторонних предела.

Точку разрыва называют точкой разрыва второго рода, если хотя бы один односторонний предел в этой точке не существует (или бесконечен).

В рассмотренном примере № 3 функция имеет в точке х =1 точку разрыва первого рода.

График этой функции состоит из двух полупрямых у=х (для х < 1) и у =3– х (для х ³ 1).

Рис. 21.

 

При исследовании функции на непрерывность точку разрыва следует искать там, где функция не определена, или в точках, где одно аналитическое выражение функции меняется на другое.

Укажем некоторые свойства непрерывных функций.

1. Если функции ƒ(х) и φ (х) непрерывны в точке х ₀, то непрерывны в точке х₀ функции ƒ(х)± φ (х), ƒ(х)· φ (х), .

Заметим, что непрерывна в точке х ₀ только, если φ (х ₀)¹0.

2. Каждая элементарная функция непрерывна в своей области определения.

3. Непрерывная на отрезке функция принимает на этом отрезке свое наибольшее и свое наименьшее значения.

4. Если функция ƒ(х) непрерывна на отрезке [ а, b ] и ƒ(а)= А, ƒ(b)= В, то каково бы ни было число С (А < С < В), найдется точка х=с внутри отрезка [ а, b ] такая, что

 

ƒ(с)= С

 

То есть функция принимает на отрезке все промежуточные значения.

5. Если функция ƒ(х) непрерывна на отрезке [ а, b ] и принимает на концах его значения разных знаков (ƒ(а)·ƒ(b) < 0), то внутри отрезка найдется точка х=с такая, что ƒ(с)=0. Это свойство позволяет приближенно находить корень уравнения, т. к. если ƒ(с)=0, то с – решение уравнения ƒ(х)=0.

Неопределенности

Теоремы о пределах функций, о бесконечно малых функциях облегчают нахождение пределов. Рассмотрим так называемые неопределенные выражения, когда эти теоремы не применимы. Например, теорема о пределе частного не применима для отношения двух бесконечно малых или двух бесконечно больших функций.

Пусть α (х) и β (х) – бесконечно малые при ; u (x)и v (x) – бесконечно большие при х®х₀. Тогда можно рассматривать пределы при х®х₀ таких, неопределенных для х=х₀, выражений (называемых неопределенностями):

α(х)·u(x), u(x)–v(x), которые условно обозначают символами , 0·∞, ∞–∞.

Раскрытие неопределенностей (т. е. нахождение пределов неопределенных выражений) происходит с применением некоторых простейших приемов, которые позволят применить теоремы о пределах.

Рассмотрим эти приемы на примерах.

Пример 1.

Здесь применима теорема о пределе частного. К этому же выражению при х® теорема о пределе неприменима, т. к. и .

представляет собой неопределенность вида .

Разложим на множители квадратный трехчлен.

9 х ²+8 х –1=9·(х – )·(х +1).

Для этого достаточно найти корни х ₁ и х ₂ квадратного трехчлена

 

ах ²+ bх + с = а (х – х ₁)·(х – х ₂).

 

Под знаком предела сократим одинаковые множители и перейдем к пределу:

 

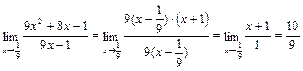
Пример 2.

 

.

 

Обнаружив неопределенность (так это в примере и записывают), раскладываем многочлены в числителе и в знаменателе на множители.

Сократив на х –1, получили дробь , числитель которой стремится к конечному пределу, отличному от нуля (), а знаменатель при х ®1 является бесконечно малой, тогда дробь при х®1 является бесконечно большой.

Пример 3.

.

Здесь числитель и знаменатель не имеют конечных пределов, имеем неопределенность . Поделив одновременно числитель и знаменатель на х ³, получим

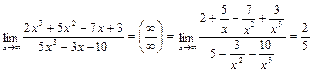, т. к. каждая из дробей является бесконечно малой и стремится к нулю.

Пример 4.

, так как

.

Для раскрытия неопределенности следует числитель и знаменатель разделить на одну и ту же старшую степень переменной.

Неопределенности вида 0·∞ и ∞–∞ приводятся к неопределенностям или .

Пример 5.

 

После приведения данных дробей к общему знаменателю была получена дробь, представляющая собой неопределенность .

Пример 6.

.

Здесь удалось избавиться от разности ( –2), стремящейся к нулю при х ®4, разложив х –4 на множители по формуле разности квадратов.

Пример 7.

В этом примере нужно было избавиться от радикалов, для чего умножили и числитель и знаменатель на сумму – сопряженное числителю выражение. Применив формулу разности квадратов в числителе, мы избавились от радикалов:

 

.

 

Пример 8.

При вычислении пределов выражений, содержащих тригонометрические функции, используется первый замечательный предел:

Чтобы подчеркнуть, что первый замечательный предел представляет собой неопределенность , т. е. отношение двух бесконечно малых, записывают его формулу в виде:

,

если α(х) – бесконечно малая функция. Заметим, что, например, не является замечательным пределом.

 

Пример 9.

.

При вычислении этого предела прежде всего обнаружили неопределенность . Чтобы использовать первый замечательный предел, разделим sin3 πх (и умножим) на 3 πх, затем и знаменатель sin πх разделим (и умножим) на πх. Сократив общие множители вынесем множитель 3 и, перейдя к пределу в числителе () и в знаменателе (), получим искомый предел.

Пример 10.

.

Принимая = α (х) (бесконечно малая при х ®∞), используем

.