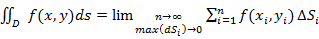Теорема 1: Теорема Абеля.
Пусть ряд 
сходится в точке 
. Тогда он сходится при любом 
, удовлетворяющем неравенству 
, причём на любом отрезке внутри интервала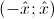 
сходимость равномерная.
Теорема 2: Теорема о радиусе сходимости.
Для каждого степенного ряда существует 
, удовлетворяющее свойствам:
1. Если 
, то ряд сходится только при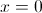 
.
2. Если 
, то ряд сходится при любых 
.
3. Если 
, то ряд сходится при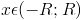 
и расходится при 
.
Сходимость на любом отрезке внутри интервала 
равномерная.
Число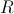 
- радиус сходимости степенного ряда.
Ряды Тейлора и Маклорена.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяется выражением
Если приведенное разложение сходится в некотором интервале x, т.е.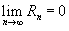 
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена:
86.Разложение в ряд Маклорена функций ln(1+x), cos x.
87. Разложение в ряд Маклорена функций ex, sin x.
Применение рядов в приближенных вычислениях.
(1) и требуется хотя бы приближенно, вычислить значение f(x) для каких – либо значений x, то естественно пользоваться приближенными формулами f(x)≈Sn(x) (2) гдеSn(x)-частичная сумма ряда. При вычислении по формулам (2) может быть достигнута любая точность в силу равенства (1), но возможно, что потребуется брать Sn(x) с очень большим номером n. Не всегда легко оценивать прогрешнсть формулы (2) это посто сделать для знакочередующегося ряда, но если ряд не знакочередкющийся, а например положительный то приходится подтыскивать мажорантный ряд для него n-го остатка данного ряда и подыскивать еготак чтобы его сумма легко вычислялась
Если ряд (1) настолько медленно сходится, что не пригоден для приближенного вычисления его суммы f(x) то обычно стараются построить другой более быстро сходящийся ряд с той же суммой f(x)
Двойные интегралы. Основные понятия и определения.
Двойным интегралом от функции 
по ограниченной замкнутой области 
называется предел интегральной суммы, построенной для функции при неограниченном увеличении числа разбиений области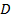 
на ячейки ( 
) и при стягивание каждой ячейки в точку ( 
), если такой предел существует и не зависит от способа разбиения области 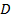на ячейки, ни от выбора 
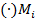в каждой из них.
Теорема существования:
Для всякой непрерывной функции в ограниченной замкнутой
области 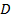существует двойной интеграл: 
