График дифференцируемой функции 
называется выпуклым вниз на интервале (a;b), если он расположен выше любой ее касательной на этом интервале. График функции называется выпуклым вверх на интервале (a;b), если он расположен ниже любой ее касательной на этом интервале.
Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы.
Теорема: Если функция во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. 
, то график функции в этом интервале выпуклый вверх. Если же 
;b) – график выпуклый вниз.
42.Точки перегиба. Необходимое условие существования точки перегиба
Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба.
В окрестности такой точки X0 график функции y = f (x) слева и справа от точки X0 имеет разные направления выпуклости.
Необходимое условие существования точки перегиба:
Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x0, f(x0)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x0) = 0.
Необходимые условия наличия перегиба:
либо 
не существует
Достаточное условие существования точки перегиба
Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x0 интервала (a, b), за исключением, быть может самой точки х0, а график функции имеет касательную в точке С = (х0, f (x0)). Если при переходе через точку х0 вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x).
Достаточные условия наличия перегиба:
1. Если 
меняет знак при переходе через точку x0, то x0 - точка перегиба.
2. Если 
то при n четном x0 -
точка перегиба, при n нечетном x0 не является точкой перегиба.
Асимптоты графика функции
Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различают вертикальные, наклонные и горизонтальные асимптоты.
Вертикальной асимптотой графика функции y=f(x) называется вертикальная прямая 
, если lim (x→a) f(x)=∞ или lim (x→a+0) f(x)=∞, или lim (x→a-0) f(x)=∞.
Наклонной асимптотой графика функции y=f(x) при x→+∞ называется прямая y=kx+b, если выполнены два условия: 1) некоторый луч (a; +∞) целиком содержится в D(f); 2) расстояние по вертикали между графиком и прямой стремится к 0 при x→+∞ 
Наклонной асимптотой графика функции y=f(x) при x→ - ∞ называется прямая y=kx+b, если выполнены два условия: 1) некоторый луч (-∞; a) целиком содержится в D(f); 2) расстояние по вертикали между графиком и прямой стремится к 0 при x→ - ∞ 
В случае, если наклонная асимптота расположена горизонтально, то есть при k=0, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая y=c=const является горизонтальной асимптотой графика y=f(x) при x→+∞ или x→-∞, если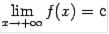 
или 
соответственно.
45. Общая схема исследования функции и построения графика
Исследование функции у = f (х) целесообразно вести в определен-1н>й последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями координат.
3. Найти интервалы знакопостоянства функции (промежутки, на Которых f(х) > 0 или f(х) < 0).
4. Выяснить, является ли функция четной, нечетной или общего Ища.
5. Найти асимптоты графика функции.
6. Найти интервалы монотонности функции.
7. Найти экстремумы функции.
8. Найти инторвачы выпуклости и точки перегиба графика функции.
На основании проведенного исследования построить график функции. Заметим, что приведенная схема исследования не является обязательной.
