Если ф-ия u=α(x) имеет производную ux’ в точке х, а ф-ия y=f(u) имеет yu’ в соответствующей точке u=α(x), то сложная ф-ия y=f(α(x)) имеет производную yx’ в точке х, кот. Нах-ся по фор-ле yx’=yu’ux’. Для нахождения производной сложной ф-ии надо производную данной ф-ии по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Теорема: Если ф-ия y=f(x) строго монотонна на интервале (а;в) имеет неравную 0 производную f’(x) произвольной точке этого интервала, то обратная ей ф-ия x=α(y) также имеет производную α’(Y) в соответствующей точке, определяемую равенством α’(y)=1/f’(x) или xy’=1/yx’. Производная обратной ф-ии равна обратной величине производной данной ф-ии.
26. Дифференцирование неявных и параметрически заданных функций
Если ф-ия задана ур-ем y=f(x), разрешенным относительно у, то ф-ия задана в явном виде(явная ф-ия). Под неявным заданием ф-ии понимают задание ф-ии в виде ур-я F(x;y)=0, неразрешенного относительно у. всякую явно заданную ф-ию у=f(x) можно записать как неявно заданную ур-ем f(x)-y=0, но не наоборот. Если неявная ф-ия задана ур-ем F(х;у)=0, то для нахождения производной от у по х нет необходимости разрешать ур-е относительно у: достаточно продифференцировать это ур-е по х, рассматривая при этом у как ф-ию х, и полученное затем ур-е разрешить относительно у’. Зависимость между аргументом х и ф-цией у задана параметрически в виде 2-х ур-ий 
Где t-вспомогательная переменная, называемая параметром. Yx’=y’t*1/xt’ т.е. yx’=yt’/xt’ - эта фор-ла позволяет находить производную yx’ от ф-ии заданной параметрически, не находя непосредственной зависимости у от х.
27. Производные основных элементарных функций
1.Степенная ф-ия y=xn, n € Ν: (xn)’=n*xn-1
2. Показательная ф-ия y=ax, a ›0, a≠1: (ax)’=axlna
3.Логарифмическая ф-ия y=loga x, a›0,a≠1: (loga x)’ =1/x*ln a
4. тригонометрическая ф-ия y=sin x, y=cosx, y=tg x, y=ctg x:
(Sin x)’=cos x*x;
(cos)’= -x’sin x;
(tg x)’= x’/cos2 x;
(ctg x)’= -x’/sin2x
28. Производные высших порядков
Производная y’=f(x) ф-ии y=f(x) есть также ф-ия от х и наз-ся производной первого порядка. Если ф-ия f’(x) дифференцируема,то ее производная наз-ся производной 2-го порядка и обозначается уn. Итак, yn=(y’)’
Производная от производной 2-го порядка, если она сущ-ет, наз-ся производной 3-го порядка и обознач-ся ym. Итак, ym=(y’)’
Производная n-го порядка наз-ся производная от производной (n-1) порядка: y(n)=(y(n-1))’
Производные порядка выше первого наз-ся производными высших порядков. Начиная с производной 4-го порядка, производные обозначают римскими цифрами или числами в скобках (yv или у(5) – производная 5-го порядка).
Дифференциал функции
Пусть y = f (x) дифференцируемая функция, т. е. она имеет конечную производную. Тогда на основании теоремы 1.3 о представлении функции в виде суммы предела и бесконечно малой функции можно записать
=> 
=> 
,
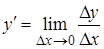где 
-бесконечно малая функция по сравнению с D x, т. е.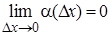 
.
Обозначим через 
произведение бесконечно малых функций и D x. Следовательно, является бесконечно малой более высокого порядка малости по сравнению с D x, 
. Запишем
.
Обозначают первое слагаемое в этой сумме через dy, т. е. 
, и называют дифференциалом функции y = f (x).
Если функция y = x, то 
. Это значит, что дифференциал dx и приращение D x независимой переменной совпадают dx = D x.
Тогда дифференциал функции имеет вид
или 
,
а приращение функции равняется
.
Из равенства следует, что производная функции равняется
.
Определение. Дифференциалом функции y = f (x) в точке 
при бесконечно малом приращении независимой переменной D x называется бесконечно малая функция dy прямо пропорциональная D x и отличающаяся от приращения функции D y на бесконечно малую функцию b(D x) более высокого порядка малости по сравнению с D x.
Так как 
, где , то дифференциал называют главной линейной частью приращения функции.
30. Понятие дифференциала функции
Дифференциалом ф-ии у=f(x) в точке х наз-ся главная часть ее приращения, равная произведению производной ф-ии на приращение ергумента, и обознач-ся dy: Dy=f’(x)*∆x Дифференциал dy наз-ют также дифференциалом 1-го порядка. Дифференциал независимой переменной равен приращению эьлй переменной: dx=∆x. Поэтому ф-лу можно записать так: Dy=f’(x)dx Дифференциал ф-ии равен произведению производной этой ф-ии на дифференциал независимой переменной. Дифференциал ф-ии y=f(x) в точке х равен приращению ординаты касательной к графику ф-ии в этой точке, когда получит приращение ∆х
