Рассмотрим для примера функцию
от двух переменных, которую будем предполагать дифференцируемой.
Мы хотим вычислить эту функцию в точке 
, где
,
,
Приближенные значения этих чисел запишем в виде конечных десятичных дробей
,
.
Таким образом, имеют место приближенные равенства
с абсолютными погрешностями приближения, удовлетворяющими неравенствам
.
Подставив в функцию 
вместо 
соответственно 
, получим приближенное равенство
с абсолютной погрешностью
,
которую при достаточно малых 
можно приближенно заменить дифференциалом функции в точке :
.
Отсюда получаем неравенство
.
| 73. Частные производные первого порядка |
Определение.Если существует конечный предел отношения частного приращения по x функции f(x,y,z) в точке M0(x0,y0,z0) к вызвавшему его приращению Δx при Δx  0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М0 и обозначается одним из символов:
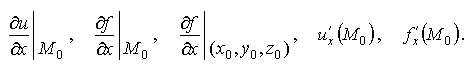По определению,
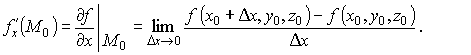Частные производные по y и по z определяются аналогично:
Производные f'x, f'y, f'z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными.
Так как частное приращение Δxf(M0) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'x(M0) может рассматриваться как производная функции f(x,y0,z0) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x.
Аналогично вычисляются частные производные по другим независимым переменным.
Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция.
|
Производная по направлению. Градиент.
Градиент. Производная по направлению представляет собой скалярное произведение вектора 
и вектора с координатами 
, который называется градиентом функции 
и обозначается 
. Поскольку 
, где 
- угол между и , то вектор указывает направление скорейшего возрастания функции , а его модуль равен производной по этому направлению.
Экстремум функции двух переменных. Основные понятия
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной (см. п. 25.4).
Пусть функция z = f(x;у) определена в некоторой области D, точка N(x 0 ;y 0 ) Î D.
Точка (х 0 ;у 0 ) называется точкой максимума функции z = f(x;y), если существует такая δ-окрестность точки (х 0 ;у 0 ), что для каждой точки (х;у), отличной от (х 0; у 0), из этой окрестности выполняется неравенство f(х;у)<f (x 0; y 0).
Аналогично определяется точка минимума
функции: для всех точек (х;у), отличных от (x 0; y 0), из δ-ξкрестности точки (x 0; y 0) выполняется неравенство: f(x;y) > f(x0;y0).
На рисунке 6: N1 - точка максимума, а N2 - точка минимума функции z = f(x;y).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (x0;y0) сравнивается с ее значениями в точках, достаточно близких к (x 0; y 0). В области D функция может иметь несколько экстремумов или не иметь ни одного.
