О п р е д е л е н и е. Ряды с положительными членами – это ряды, члены которых не отрицательны.
Рассмотрим числовой ряд 
,
где 
для такого ряда 
. Значит, последовательность частичных сумм возрастает.
Из теоремы о пределе монотонной последовательности можно сформулировать условие сходимости ряда с положительными членами.
Ряд с положительными членами всегда имеет сумму и эта сумма конечна, а ряд будет сходящимся, если частичные суммы ряда ограничены сверху, и бесконечна, а ряд расходящимся в противном случае.
Достаточные признаки сходимости рядов с положительными членами.
Теорема 1 (признак сравнения). Если члены двух числовых рядов 
и 
удовлетворяют неравенству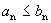 
для любых n, то из сходимости второго ряда следует сходимость первого ряда. Из расходимости первого ряда следует расходимость второго ряда.
Пример. Рассмотрим ряд 
. Сравним его с гармоническим рядом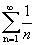 
.
, 
.
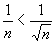По признаку сравнения данный ряд расходится.
Теорема 2 (признак Даламбера). Если для числового ряда существует конечный предел отношения последующего члена ряда к предыдущему
, то:
а) при 
ряд сходится;
б) при 
ряд расходится;
в) при 
вопрос о сходимости открыт.
Знакочередующиеся ряды. Абсолютная и условная сходимости.
Понятие знакопеременного ряда включает в себя как знакочередующиеся ряды, так и ряды с произвольным чередованием знаков своих членов.
Знакопеременный ряд 
сходится, если сходится ряд 
.
В этом случае знакопеременный ряд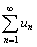 
называют абсолютно сходящимся.
Сходящийся знакопеременный ряд 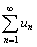называют условно сходящимся, если ряд 
расходится.
Пример. Исследовать на сходимость знакопеременный ряд
Решение:
.
Исследуем на сходимость положительный ряд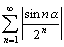 
.
Воспользуемся признаком сравнения 1:
.
Ряд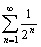 
– сходящаяся бесконечно убывающая геометрическая прогрессия.
По признаку сравнения ряд 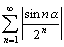сходится, поэтому знакопеременный ряд 
является абсолютно сходящимся.
Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.:
Признак Лейбница.
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда
выполняются следующие условия:
1.  (монотонное убывание {an})
2.  .
Тогда этот ряд сходится.
|
Степенные ряды. Область сходимости степенного ряда.
Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
Часто рассматривается также ряд, расположенный по степеням (x − x0), то есть ряд вида
где x 0 − действительное число.
