Если график функции задан в полярной системе координат, для того чтобы вычислить площадь криволинейного сектора, ограниченного двумя лучами 
и графиком функции 
в полярной системе координат, томожно использовать метод интегральных сумм, вычисляя площадь криволинейного сектора как предел суммы площадей элементарных секторов, в которых график функции заменен дугой окружности 
. Можно использовать и метод дифференциалов: 
.
Заменяя элементарный криволинейный сектор, соответствующий центральному углу 
круговым сектором, имеем пропорцию 
. Отсюда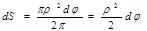 
. Интегрируя и используя формулу Ньютона – Лейбница, получается 
.
Приложение определенного интеграла..Вычисление длины дуги плоской кривой.
Если дуга представляет собой график непрерывно дифференцируемой функции 
, дифференциал длины дуги можно вычислить по формуле
. Поэтому 
Если гладкая дуга задана параметрически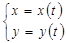 
, то 
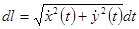. Получается, 
.
Если дуга задана в полярной системе координат, то
.получается, у 
.
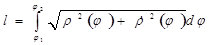После того, уберите ручкой символ «&» в формулах, а то не поймем.
Приложение определенного интеграла. Вычисление объема тела.
1.Вычисление объемов тел по площадям параллельных сечений. Для вычисления объеам некоторого тела V по известным площадям сечений 
этого тела плоскостями, перпендикулярными прямой OX, проведенными через любую точку x отрезка [a, b] прямой OX.
Считая элементарный объем 
, над отрезком 
объемом прямого кругового цилиндра с площадью основания и высотой 
, получится 
, применяем формулу Ньютона – Лейбница, получим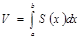 
.
2.Вычисление объемов тел вращения. Для определения объема тела вращения вокруг оси OX. Тогда 
. объем тела вращения вокруг оси OY, если функция задана в виде 
, можно вычислить по формуле 
.
Если функция задана в виде 
и требуется определить объем тела вращения вокруг оси OY, формулу для вычисления объема получим следующим образом
имеем 
. Интегрируем и применяем формулу Ньютона – Лейбница, и получается 
.
Функции нескольких (двух) переменных. Основные понятия
Переменная z (с областью изменения Z)называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.
Обозначения: z = f(x,y), z = z(x,y). Переменная z (с областью изменения Z)называется функцией нескольких независимых переменных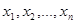 
в множестве М, если каждому набору чисел 
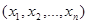из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных. Обозначения: z = f 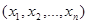, z = z .
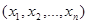