Если функция F(x) является первообразной ф-ии f(x) на (a,b), то множество всех первооб-х для f(x) задается формулой F(x)+C, где С-постоянное число.
Множество всех первооб-х ф-ий F(x)+C для f(x) наз-ся неопределнным интегралом от ф-ии f(x) и обозначается символом ∫f(x)dx. Таким образом, по определению ∫f(x)dx=F(x)+C.
Операция нахождения неопределенного интеграла от ф-ии наз. интегрированием этой ф-ии.
Свойства неопределенного интеграла
1. Дифференциал от неопределённого интеграла равен подынтегральному выражению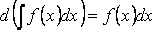 
2. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы 
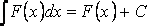3. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов 
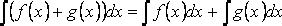4. Постоянный множитель можно выносить за знак интеграла 
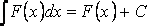5. Если , то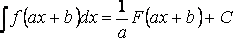 
Таблица основных неопределенных интегралов
49. Основные методы интегрирования (метод интегрирования подстановкой)
Метод подстановки (замена переменной). Если удается свести подинтегральное выражение к виду f(ų(t) ų’(t)dt и известен ∫d(x)dx=F(x)+C, то интеграл ∫f(ų(t)ų’(t)dt= F(ų(t))+C. Иногда приходится исходную переменную выражать через дифференциальную ф-ию: ∫f(x) dx, x=ų(t), dx= dų(t)=ų’(t)dt. Др. словами, формулу интегрирования подстановкой можно применять справа налево.
50. Основные методы интегрирования (метод интегрирования по частям)
Пусть u=u(x) и u=v(x) –ф-ии, имеющие непрерывные производные. Тогда d(uv)=u·dv+v·du. Интегрируя это равенство, получим ∫d(uv)=∫u·dv+∫v·du или ∫u·dv=uv-∫v·du - формула интегрирования по частям. 1.Если в произведении одним из множителей явл log или arc ф-ии, то за u берут их, а все ост-ые принять за dv. 2.Если не Iog, не arc ф-ий нет, то за u берут степенную ф-ю. 3.Если под знаком интеграла стоит произведение показат-ой ф-ии на тригонометрич-ую, то нет разницыЭ, что принять за u.
Простейшие дроби 4 типов.
Дробь вида P(x)/Q(x), где Pn(x) и Qm(x) являются многочленами степени n и m, называется рациональной. Если показатель степени числителя больше показателя степени знаменателя, то дробь называется неправильной, в противном случае — правильной. Правильные рациональные дроби вида: (I). A/x-a; (II). A/(x-a)ⁿ (n≥2, nЄ N); (III). Mx+N/x²+px+q (корни знаменателя комплексные, т.е p²-4q<0); (IV). Mx+N/(x²+px+q)ⁿ (n≥2, корни знамен. компл-е), где A, a, M, N, p, q - действительные числа, наз-ся простейшими рациональными дробями I, II, III и IV типов.
52. Интегрирование рациональных функций.
Опр. Рациональной называется функция вида Pm(x)/Qn(x) где Pm и Qn есть многочлены порядков m и n соответственно Pm (x)= amxm + am-1xm-1 +..a1x + a0; Qn(x)= bnxn + bn-1xn-1+..b1x+b0;am, bn = 0. Дробь Pm(x)/Qn(x) наз-ся правильной если порядок числителя меньше порядка знаменателя. Любую правильную дробь можно представить в виде суммы простейших дробей 4-х видов. Опр. Простейшими дробями наз-ся дроби вида A/ x-a; B/ (x-a)k; Cx + D/ x2 +px+g; Mx +N/ (x2+px-g)n; интеграл от простейшей дроби: ∫ A/x-a(dx писать на ровне с дробью)= A∫ dx/ x-a=∫d(x-a)/x-a= Aln|x-a|+C.
