Рівняння виду
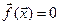, (1)
де 
- вектор багатомірного аргументу 
називають скінченими рівняннями. Сюди належать системи лінійних і нелінійних алгебраїчних рівнянь, алгебраїчні й трансцендентні рівняння однієї змінної.
У розгорнутому вигляді запишемо:
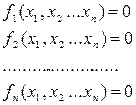
(2)
У випадку однієї змінної (1) й (2) перетворюються у f(x)=0.
Деяке числове значення , яке задовольняє рівняння (1), називається розв’язкою, або розв’язанням.
Методи розв’язування рівнянь поділяються на аналітичні, графічні та чисельні. Крім того, розрізняють точні та наближені методи.
Точні – це аналітичні, які дають розв’язання за алгоритмом зі строго визначеною кількістю кроків при абсолютно точних обчисленнях.
До наближених відносять чисельні та графічні методи.
Найефективнішими наближеними методами розв’язування рівнянь є чисельні. Суть їх полягає у послідовних уточненнях деяких грубих, так званих нульових наближень розв’язання 
.
Якщо процес уточнення збіжний, тобто послідовні наближення прямують до певного стійкого значення, розв’язання 
на k-му кроці обчислень та знаходження коренів рівнянь можна здійснювати як завгодно точно. Ця особливість, а також простота програмної реалізації і визначили їх дальше найширше використання.
Вивчення методів розв’язування скінчених рівнянь має надзвичайно важливе значення для задач електроенергетики. Практично у всіх задачах аналізу, синтезу й керування енергетичних систем і їх елементів виникає необхідність розв’язання різних типів скінчених рівнянь.
До чисельних відноситься метод половинного ділення.
Метод половинного ділення
Для знаходження кореня 
рівняння f(x)=0, відділеного в проміжку [a;b],проміжок ділять навпіл. Якщо 
, то 
― корінь рівняння. Інакше вибирають половину проміжку 
чи 
, на кінцях якого функція має протилежні знаки. Новий проміжок знову ділять пополам.
Метод хорд
Інтервал відділення кореня [a;b] під час його уточнень ділиться пропорційно значенням функції на границях інтервалу у відношеннях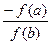 
(“-“ тому, що f(a)f(b)<0). Тоді:
. (*)
Отже, функція замінюється хордою, яка перетинає функцію в точках, що відповідають границям абсцис інтервалу.
Наступні уточнені значення кореня 
знаходять шляхом послідовного застосування (*) до того з відрізків 
, для якого 
аж до досягнення заданої точності.
Абсолютна похибка відхилення наближеного значення 
на k-му кроці обчислень від дійсного кореня :
,
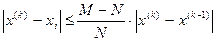де M, N – найбільше та найменше значення модуля похідної df(x)dx в інтервалі 
.
Метод простої ітерації (послідовного наближення)
f(x)=0 
x =φ(x)
Підставимо значення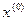 
, одержимо нове значення кореня 
і т.д.
.
Метод Ньютона (дотичних)
,
де 
 | |||
 |
§ 5.2. Аналітичні методи розв’язування системи лінійних рівнянь
У випадку лінійної системи рівнянь вектор-функція (1) набирає вигляду матрично-векторного рівняння:
, (4)
. (3)
Якщо А – неособлива (det≠0), то (3) має єдиний розв’язок:
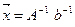, (5)
де 
; 
,
в якій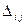 
- алгебраїчні доповнення елементів 
транспонованої матриці коефіцієнтів рівняння (3).
При високих порядках (4) пряме знаходження оберненої матриці 
вимагає виконання великого обсягу обчислень з необхідністю визначення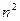 
алгебраїчних доповнень.
Шляхом простих перетворень (5) одержуємо розв’язання (3) у вигляді алгоритму Крамера, згідно з яким вектор-стовпець невідомих:
, (6)
де 
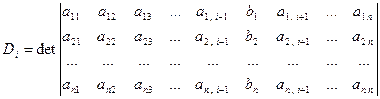, (7)
який одержується з матриці коефіцієнтів А шляхом заміни її і -го стовпця вектор-стовпцем вільних членів b.
У формулі (6) здійснюється n-разове розкриття детермінанта (7) матриці n-го порядку, тоді як у (5) 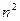разів розкриваються детермінанти матриці (n-1)-го порядку. Оскільки з погляду розкриття детермінанту n-го порядку виконується стільки ж операцій, що й під час розкриття (n-1)-го порядку, то з погляду обсягу обчислень формули (5) і (6) рівноцінні й дуже трудомісткі. Тому розробленні прямі методи розв’язання (3): методи Гауса, метод квадратних коренів, метод Халицького й інші.
§ 5.2.1 Метод Гауса
Суть методу – методу послідовних виключень – полягає у зведенні матриці (3) до трикутної (верхньо- чи нижньо-трикутної) – прямий хід виключень чи до діагональної - прямий і зворотний хід виключень.
Для зведення матриці рівняння (3) до трикутної необхідно виконати поетапне множення цього рівняння на n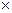 
n - мірну матрицю, значення елементів якої залежить від порядкового номера компонента 
.
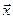Для 
необхідно рівняння помножити зліва на матрицю.
,
тоді отримаємо 
або 
для 
одержимо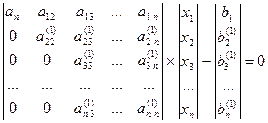 
В результаті отримаємо:
. (8)
Зведення вихідного рівняння до вигляду (8) називається “прямим ходом”, дії якого полягають у перемноженні цього рівняння почергово на матриці 
, що перетворюють матрицю А верхню трикутну. Використовуючи (8), можна знайти всі компоненти 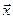, починаючи від 
.
В результаті здійснення оберненого ходу (множення почергово на матриці 
). А рівняння (3) зводиться до діагональної:
отримуємо рівняння, яке множимо на 
.
В результаті отримуємо:
.
Для визначення вектора х необхідно (9) перемножити на матрицю:
.
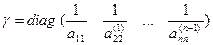§ 5.2.2 Ітераційні методи
1) Метод простої ітерації.
Для застосування простої ітерації f(x)=0 запишемо у вигляді:
,
де 
- діагональна від А;
або 
Компактно: 
. (*)
Процес простої ітерації полягає у поступовому підставленні в праву частину рівняння (*) попереднього наближення, що на k+1-му кроці обчислень здійснюється за формулою:
.
За нульове наближення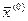 
, коли не відомі додаткові умови, приймають вектор 
, тобто = .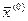
У процесі ітерації дістаємо послідовність наближень:
Для одержання розв’язання рівняння необхідно, щоб обчислення було збіжним, тобто значення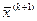 
при необмеженому зростанні k повинно прямувати до певної границі.
Достатньою умовою збіжності є те, що будь-яка з нормальної матриці В<1,
||В||<1
1) m – норма – найбільша сума по рядах матриці
;
2) e – норма – найбільша сума по стовпцях матриці
;
3) k – норма – дорівнює кореню із суми:
;
Метод простої ітерації має порівняно невисоку швидкість збіжності.
§ 5.2.3 Метод ітерації Зайделя
Під час знаходження наближень “старших” невідомих 
підставляємо наближене значення “молодших”, одержаних не на попередньому, а на цьому кроці (тобто не 
.
Це означає, що процес ітерації можна здійснити так:
Швидкість збіжності набагато вища.
