Комплексный двухкартинный чертеж точки. 4 страница

На горизонтальной проекции видна вся боковая поверхность конуса вращения.

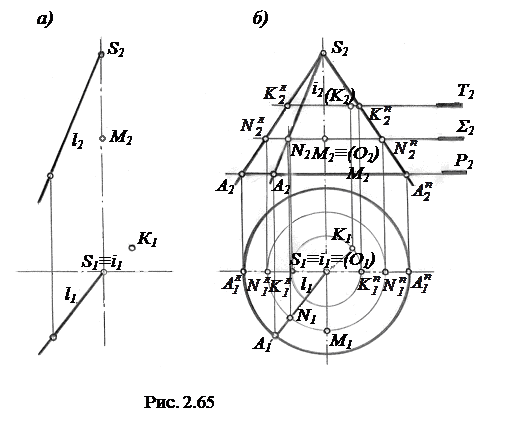
Пусть требуется построить недостающие проекции точек М и К, расположенных на поверхности конуса вращения, определитель которого W (l, i) (рис.2.65, а); требуется также построить фронтальный и горизонтальный очерки конуса.

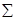Для решения задачи через М₂ проводим главную проекцию плоскости вращения так, что ^ i₂ (рис.2.65, б). Строим О₂= Ç i₂ и N₂= Ç l₂. По линии проекционной связи находим О₁ º i₁ и N₁ Î l₁. Очевидно, радиус вращения R точки N равен О₁N₁. Радиусом вращения R=O₁N₁ с центром в точке О₁ строим горизонтальную проекцию окружности вращения точки N. Фронтальная проекция окружности вращения проецируется в виде отрезка , совпадающего с , где и - соответственно фронтальные проекции точки N в крайнем левом и крайнем правом положениях относительно наблюдателя.

Фронтальные очерковые образующие конуса проходят через точки 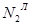, S₂ и , S₂.

Для нахождения М₁ через М₂ проводим линию проекционной связи до пересечения с построенной окружностью. Далее находим К₂. Для этого через К₁ проводим параллель радиусом R=O₁K₁, отмечаем крайнее правое (можно крайнее левое) положение и по линии проекционной связи в точке пересечения с фронтальной очерковой образующей, проходящей через точки S₂ и , находим . Проекция расположена на главной проекции Т₂ плоскости вращения точки К. На фронтальной проекции окружности вращения по линии проекционной связи находим К₂. Проекция К₂ не видна.

Очерк поверхности конуса содержит не только проекции очерковых образующих, но и проекции основания. Поэтому, обозначая некоторую точку А на образующей l и используя рассмотренный прием введения плоскости вращения Р точки А, имеем фронтальный очерк конуса в виде треугольника и горизонтальный очерк в виде окружности радиуса R=O₁A₁.

Линию на поверхности строят по точкам, задаваясь крайними точками на границе видимости (при наличии таковых), ближайшими к оси вращения и промежуточными. Следует иметь в виду, что очерковые образующие являются границей видимости. Общее количество выбранных на кривой линии точек должно быть не менее 4-6. Аналогичный подход сохраняется и для других поверхностей вращения, рассматриваемых ниже.

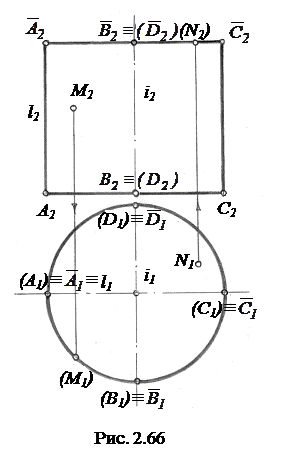
Цилиндр вращения. Имеет определитель Ф(l, i), где l – образующая прямая линия, i – ось вращения. Боковая поверхность такого цилиндра горизонтально–проецирующая, т.к. все его образующие перпендикулярны П₁ и, перемещаясь в пространстве, пересекают все точки окружности основания (рис.2.66).

Проекции образующих и вместе с проекциями верхнего и нижнего A₂B₂C₂D₂ оснований являются фронтальным очерком цилиндра. На фронтальной проекции видна часть поверхности 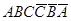и не видна . На горизонтальной проекции боковая поверхность цилиндра проецируется в окружность. Верхнее основание видно на горизонтальной проекции, нижнее ABCD не видно. Построение проекций точек М и N и их видимость показаны на рис.2.66.

 

Сфера. Имея определитель вида Ф (m, i), поверхность сферы образуется вращением полуокружности (меридиана) m вокруг оси i, проходящей через её центр и лежащей в плоскости этой полуокружности (рис. 2.67).

M2

M1

Каждая точка образующей m, в том числе и крайняя правая точка М, при вращении вокруг оси i описывают окружности. Наибольшую окружность Э (экватор) описывает точка М; горизонтальная проекция экватора Э₁ есть его натуральная величина и является горизонтальным очерком сферы (рис. 2.68).

Две другие проекции экватора проецируются в отрезки прямых

Э₂ || х₁₂ и Э₃ || у₃. При рассечении сферы фронтальной плоскостью уровня S, проходящей через центр сферы О и ее ось i, поверхность рассекается по окружности N. Горизонтальная проекция N₁ этой окружности есть отрезок прямой, равный диаметру сферы. Фронтальная проекция N₂ есть натуральная величина окружности и является фронтальным очерком сферы. Профильная проекция N₃ также представляет из себя отрезок прямой, равный диаметру сферы.

Если рассечь сферу профильной плоскостью уровня Т, проходящей через центр О и ось i, то поверхность сферы также рассечется по окружности L. Фронтальная L₂ и горизонтальная L₁ проекции ее являются отрезками прямых, равными диаметру сферы. Профильная проекция L₃ есть натуральная величина окружности и является профильным очерком сферы.

На рис. 2.68 показаны проекции точек К, Е и F, расположенных на соответствующих очерковых окружностях Э, N и L. Все проекции точек видимые, поскольку на горизонтальной проекции видно верхнее полушарие,

ограниченное экватором Э (нижнее не видно), на фронтальной проекции видно переднее полушарие, ограниченное проекцией окружности N фронтального очерка (задняя часть не видна) и на профильной проекции видно левое полушарие, ограниченное проекцией окружности L профильного очерка.

Для нахождения проекций G₁ и G₃ точки G, заданной на сфере проекцией G₂, через точку G проводим горизонтальную уровня плоскость Р, которая рассекает сферу по параллели. На горизонтальной проекции радиусом этой параллели в зоне расположения точки G проводим дугу окружности и на пересечении её с линией проекционной связи, проведенной из точки G₂, находим G₁. Проекция G₃ расположена на линии проекционной связи, проведенной из точки G₂, на расстоянии Dу от i₃. Проекции G₁ и G₃ не видны.

Если задана G₁ и необходимо найти G₂ и G₃, то построения проводят в обратном порядке.

Тор. Имеет определитель вида Ф (а, i), где а – окружность или часть ее, i – ось вращения. Поверхность тора образуется вращением окружности а или части ее вокруг оси i, лежащей в плоскости окружности или ее дуги и не проходящей через центр О (рис. 2.69).

В зависимости от расположения оси i относительно образующей а имеем различные разновидности поверхностей торов. Если ось i лежит вне окружности (рис. 2.69, а), то образуется открытая торовая поверхность, похожая на поверхность баранки. Если ось i пересекается с дугой окружности или её продолжением, то может получится вогнутая (рис. 2.69, б) или выпуклая (рис. 2.69, в) закрытая торовая поверхность.

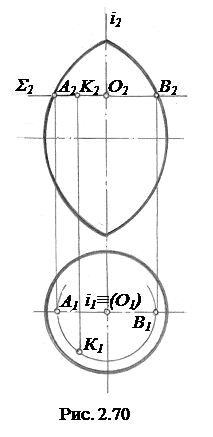
Пусть требуется найти горизонтальную проекцию К₁ точки К, расположенной на поверхности тора, заданного фронтальным и горизонтальным очерками (рис. 2.70). Тогда через точку К проводим плоскость вращения 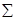^ i, которая рассекает поверхности по окружности, фронтальная проекция которой есть отрезок прямой А₂В₂. Радиусом R=О₂А₂=О₂В₂ строим горизонтальную проекцию параллели – окружность, на пересечении с которой линии проекционной связи, проведенной из точки К₂, находим проекцию К₁. Проекция К₁ видимая, т.к. лежит на верхней половине тора выше экватора.

Если задана проекция К₁, и надо найти проекцию К₂ , то построение выполняем в обратном порядке.

ПОЗИЦИОННЫЕ ЗАДАЧИ

Это задачи, в которых решается вопрос о взаимном порядке, взаимном положении и взаимном пересечении геометрических объектов.

Задачи на взаимный порядок и взаимное положение геометрических объектов, а также задачи на взаимную принадлежность геометрических объектов были разобраны в разделах 1и2.Эти задачи не имеют самостоятельной методики и опираются на решение других позиционных задач. Наибольший практический интерес представляют задачи на пересечение поверхностей и задачи на пересечение линии и поверхности. Изучение этих задач рассмотрим методом индукции, т. е. от частного к общему.

В этих двух типах задач можно выделить три группы задач:

1)Оба пересекающихся геометрических объекта занимают проецирующее положение;

2)Один из пересекающихся геометрических объектов занимает проецирующее положение, другой – непроецирующее;

3) Оба пересекающихся геометрических объекта занимают непроецирующие положения.

Проецирующими геометрическими объектами могут быть: прямая, плоскость, цилиндрическая поверхность (см. рис. 1.11).

Рассмотрим первый тип задач – задачи на пересечение поверхностей.

Вначале рассмотрим задачи на пересечение проецирующих геометрических объектов и когда один из объектов непроецирующий. После этого рассмотрим задачи на построение линии пересечения непроецирующих геометрических объектов.