Комплексный двухкартинный чертеж точки. 1 страница

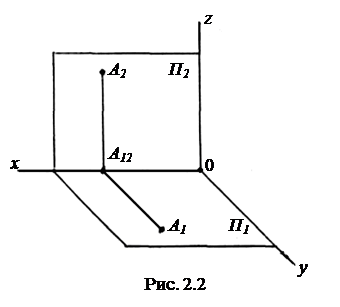Пространственная модель плоскостей проекций с заданными на них горизонтальной и фронтальной проекциями А₁ и А₂ точки А (рис. 2.2) хотя и определяет положение точки А в пространстве, но неудобна в использовании. Для того, чтобы превратить пространственную систему плоскостей проекций в плоскую фигуру, совмещаем плоскости проекций. При этом плоскость П₁, вращаясь вокруг оси x, опускается вниз до совмещения с плоскостью П₂. На рис. 2.3 изображены совмещенные плоскости проекций

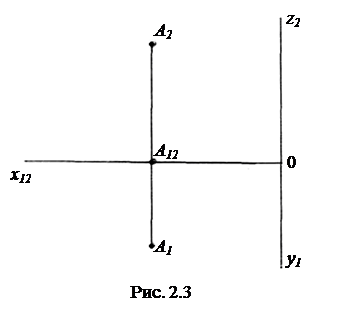и проекции точек на них.

Совмещенные плоскости проекций изображаются с помощью проекций осей координат - оси x₁₂, представляющей собой слившиеся горизонтальную и фронтальную проекции оси x, оси z₂ - фронтальной проекции оси z, и оси y₁ - горизонтальной проекции оси y. Оси z₂ и y₁ расположены вертикально по одной прямой и по разные стороны от точки О. В ряде случаев оси z₂ и y₁ не обозначают (рис. 2.4).

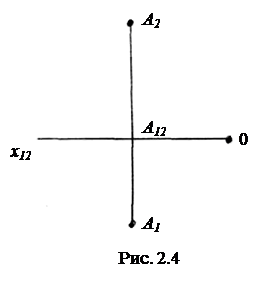Поле чертежа представляет собой проекции совмещенных плоскостей проекций, а весь чертеж является моделью трехмерного пространства.

Вместе с проекциями А₁, А₂ точки А и прямой, связывающей эти проекции, рис. 2.3 и рис. 2.4 каждый представляют собой двухкартинный комплексный чертеж точки (эпюр точки).

Впервые описал и обосновал комплексный чертеж точки, применяя совмещение плоскостей проекций, известный французский ученый Гаспар Монж, который жил и творил во времена Великой Французской революции.

Труд «Начертательная геометрия» был написан Монжем в 1775 году. В те времена метод Монжа было военной тайной, так как этот метод давал большие преимущества французской промышленности. Монжу разрешили опубликовать свой труд только в 1795 году, через 20 лет.

Метод изображения с помощью совмещения плоскостей проекций вошел в историю техники как метод Монжа.

Отличительной особенностью комплексного чертежа точки является то, что горизонтальная и фронтальная проекции точки А всегда лежат на одном перпендикуляре к горизонтальной оси x₁₂ эпюра. Действительно, порознь имеет место А₁Аx₁ x₁ и А₂Аx₂ x₂, но так как горизонтальная и фронтальная проекции оси x₁ и x₂ совпадают, образуя x₁₂, и проекции точки Аx₁ и Аx₂ совпадают, образуя А₁₂, а при вращении П₁ вокруг оси x отрезки А₁Аx₁ и А₂Аx₂ не меняют своего положения по отношению к одноименным проекциям оси x, то после совмещения получается, что из одной точки А₁₂ слившихся проекций оси x₁₂ выходят два отрезка А₁₂А₂ и А₁₂А₁ , порознь перпендикулярные к этой оси. Следовательно, эти отрезки лежат на одной прямой.

Перпендикуляр к оси эпюра, связывающий проекции А₁ и А₂, называется линией проекционной связи.

Комплексный чертеж точки вполне определяет ее положение в пространстве.

2.1.2. Замена плоскостей проекций. Плоскостей, перпендикулярных к плоскости П₁, кроме плоскости П₂, можно провести множество, и точно также к плоскости П₂ можно провести множество перпендикулярных плоскостей.

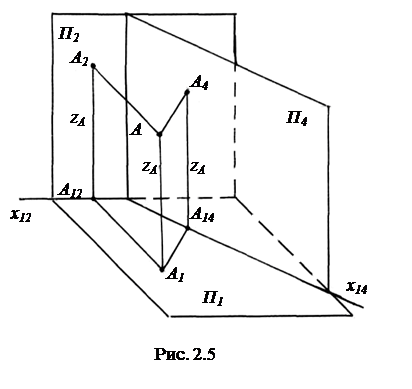
Рассмотрим, каким образом необходимо преобразовать чертеж, чтобы заменить плоскость П₂ на П₄ , причем П₄ П₁. На рис. 2.5 изображена система плоскостей проекций П₁ - П₂ с осью x₁₂. Назовем ее старой системой. Введем плоскость П₄, перпендикулярную П₁. Новая система плоскостей проекций П₁ - П₄ имеет ось проекций x₁₄. Проекциями точки А в старой системе были А₁ и А₂, а в новой системе стали А₁ и А₄. Точка А₄ получена ортогональным проецированием точки А на плоскость П₄. На осях проекций x₁₂ и x₁₄ не отмечено начало координат, потому что координата x в данном преобразовании не нужна.

При замене одной из плоскостей проекций, как видно из рис. 2.5, имеется два инварианта (величины, остающиеся постоянными при преобразованиях):

1) проекция точки на незаменённую плоскость проекций. В данном случае это точка А₁;

2) расстояние точки до незаменённой плоскости проекций. В данном случае это z_А.

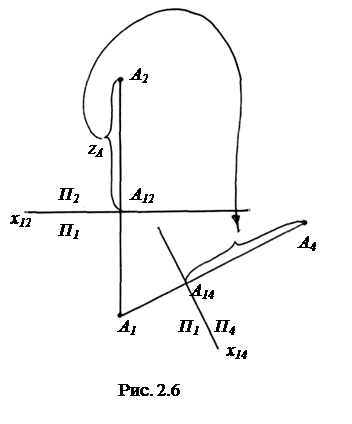
На рис. 2.6 показано построение проекции точки А₄ по данным А₁ и А₂ и имеющемуся направлению новой оси проекции x₁₄ при замене П₂ на П₄. На этом рисунке даны старая и новая оси проекций. Около каждой оси отмечены плоскости проекций, пересечением которых они являются.

Из точки А₁, которая является инвариантом при данном преобразовании, проводим линию связи перпендикулярно к оси x₁₄. От точки пересечения линии связи А₁₄ с осью x₁₄ откладываем второй инвариант - расстояние точки А до плоскости П₁. Тогда А₁₄А₄ = z_А = А₁₂А₂.

На рис. 2.7 показано преобразование чертежа, при котором заменена плоскость П₁ на П₅. Здесь инвариантами являются проекция А₂ и расстояние до незамененной плоскости П₂. Построения понятны из чертежа. Очевидно, что А₂₅А₅ = y_А = А₁А₁₂.

 

 

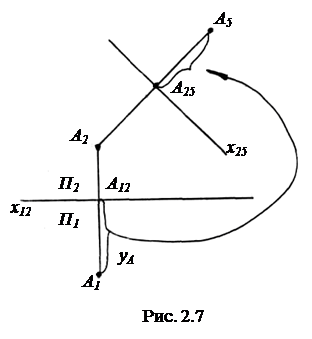
Если необходимо заменить обе плоскости проекций, то преобразование нужно выполнять последовательно: сначала заменить одну плоскость проекций, а потом вторую.

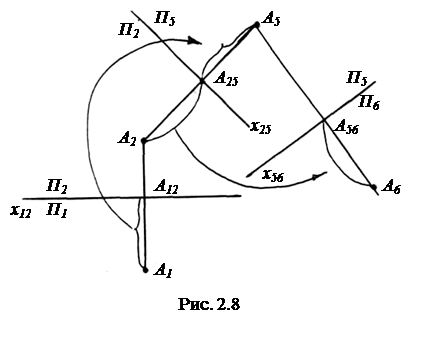
На рис. 2.8 показано преобразование, в котором система П₁ - П₂ заменена на систему П₅ - П₆. Сначала заменена плоскость П₁ на П₅, а после этого П₂ на П₆.

2.1.3. Комплексный трехкартинный чертеж точки. Оси проекций z и y (рис. 2.1) образуют плоскость, перпендикулярную к оси x и к плоскостям П₁ и П₂. Обозначим эту плоскость П₃ и назовем ее профильной плоскостью проекций.

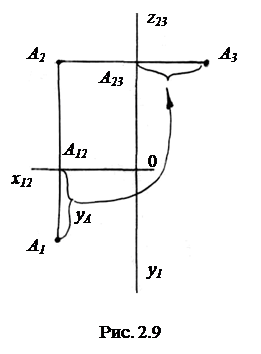Построение профильной проекции точки. Профильную проекцию А₃ точки А на плоскость П₃ найдем, заменив П₁ на П₃ (рис. 2.9).

В данном преобразовании старая система плоскостей проекций П₁ - П₂ заменяется на новую П₂ - П₃. Проекция А₂ остается неизменной. Из точки А₂ проводим линию связи, перпендикулярную новой оси проекций, и вдоль нее от новой оси откладываем второй инвариант - расстояние точки А до плоскости П₂, равное y_А = А₁А₁₂.

Новая ось проекций должна быть названа x₂₃, но, учитывая традиции в изучении начертательной геометрии и то, что новая ось совпадает с осью z, мы вместо x₂₃ напишем z₂₃.

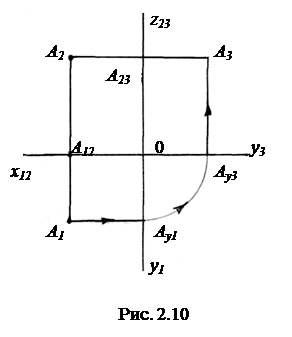
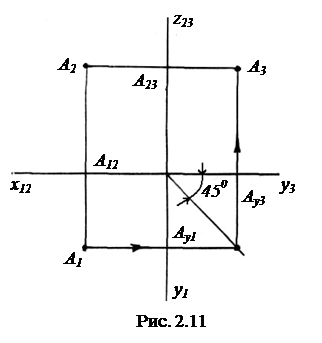
На рис. 2.10 и рис. 2.11 показаны практические приемы построения профильной проекции точки. Из точки А₂ в обоих случаях проводится линия связи, параллельная горизонтальной оси эпюра. Вдоль этой линии от точки А₂₃ откладывается отрезок, равный y_А = А₁А₁₂. На рис. 2.10 эта операция производится с помощью дуги окружности, на рис. 2.11 с помощью отражения от прямой, проведенной под углом 45⁰ к горизонтальной оси чертежа. Порядок построения показан стрелками.

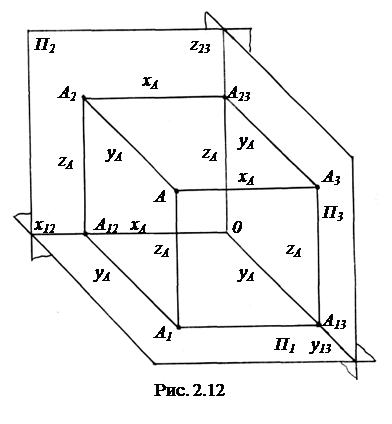
Параллелепипед координат. На рис. 2.12 показана пространственная модель плоскостей проекций и построены проекции точки А на горизонтальную - А₁, фронтальную - А₂ и профильную - А₃ плоскости проекций. Если плоскости проекций продолжить во все стороны, то они разобьют пространство на 8 частей, называемых октантами. Ограничимся рассмотрением проекций фигур, находящихся в первом октанте, которому соответствуют положительные направления осей.

При проецировании точки на плоскости проекций образуется параллелепипед, у которого три пространственных ребра АА₁, АА₂ и АА₃ совпадают с проецирующими лучами. Шесть ребер параллелепипеда лежат на плоскостях проекций - по два ребра на каждой: А₁А₁₂ и А₁А₁₃ на П₁; А₂А₁₂ и А₂А₂₃ на П₂; А₃А₁₃ и А₃А₂₃ на П₃. Эти ребра образуются пересечением плоскостей, заданных парами пересекающихся проецирующих лучей, с плоскостями проекций.

Последние три ребра совпадают с осями проекций: А₁₂О - с осью x₁₂, А₁₃О - с осью y₁₃ и А₂₃О - с осью z₂₃.

Так как данная система плоскостей проекций совпадает с прямоугольной системой координат, то полученный параллелепипед можно назвать параллелепипедом координат.

 

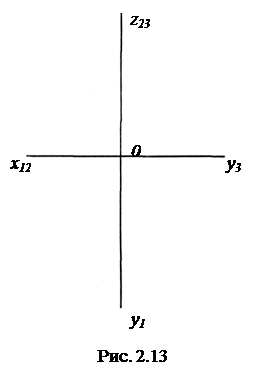
Совмещение плоскостей проекций осуществляем как и для случая построения комплексного двухкартинного чертежа точки. Плоскость П₁ при этом вращается вокруг оси x₁₂ до совмещения с плоскостью П₂, и горизонтальная проекция оси у₁ опускается вниз (рис. 2.13). Плоскость П₃ вращается вокруг оси z₂₃ вправо до совмещения с плоскостью П₂. При этом оси х₁₂ и z₂₃ остаются на месте. Профильная проекция оси у₃ поворачивается вместе с плоскостью П₃ вправо и встает на одну линию с осью х₁₂.

На рис. 2.14 показан комплексный трехкартинный чертеж (эпюр) точки А. Также как и для комплексного двухкартинного чертежа точки в данном случае имеем:

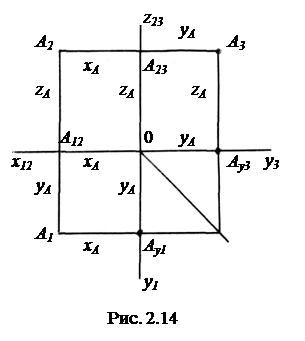
1) горизонтальная и фронтальная проекции точки А лежат на одной прямой, перпендикулярной к оси х₁₂, т.е. А₁А₂ х₁₂;

2) фронтальная и профильная проекции точки А лежат на одной прямой, перпендикулярной к оси z₂₃, т.е. А₂А₃ z₂₃. Доказательство этого положения аналогично приведенному ранее для комплексного двухкартинного чертежа точки, но только по отношению к оси z₂₃.

Проекции точек, лежащих на плоскостях проекций. Проекции точки, лежащей на плоскости, можно получить, приравнивая нулю соответствующую координату, так как координата – отрезок, выражающий расстояние от точки до плоскости проекции (рис.2.15).

Рис. 2.15

 

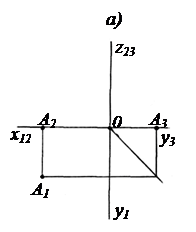
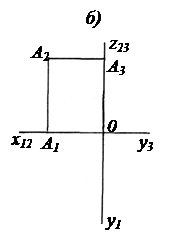
Поэтому, если z_А =0, то А П₁ (рис. 2.15, а). При у_А =0 А П₂ (рис. 2.15, б) и, когда х_А =0, А П₃ (рис. 2.15, в).

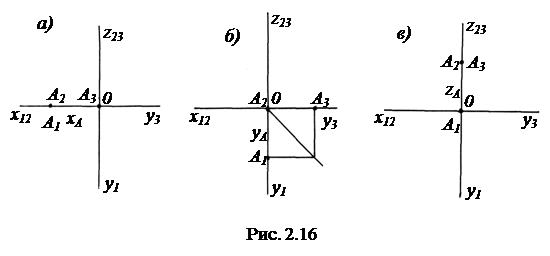
Проекции точек, лежащих на осях проекций. На рис. 2.16 рассмотрены случаи, когда точка А лежит на осях проекций: А x (рис. 2.16, а); А y (рис. 2.16, б); А z (рис. 2.16, в).

 

 

Построение проекций точек по координатам. Последовательность построения проекций точки А (x_A, y_A, z_A) следующая (рис. 2.17):

1) От точки О вдоль оси х₁₂ откладываем отрезок длиной x_A и отмечаем точку А₁₂.

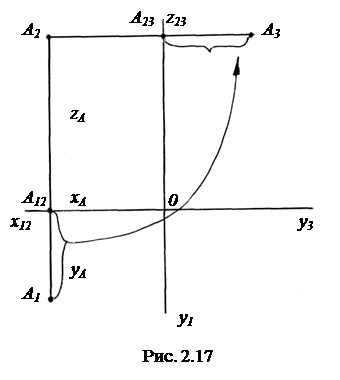2) Через точку А₁₂ проводим линию проекционной связи перпендикулярно оси х₁₂.

3) Вниз на линии проекционной связи от точки А₁₂ откладываем отрезок длиной y_A и получаем горизонтальную проекцию А₁.

4) Вверх на линии проекционной связи от точки А₁₂ откладываем отрезок длиной z_A и получаем фронтальную проекцию А₂.

5) Строим профильную проекцию А₃, для чего из точки А₂ проводим линию проек-ионной связи перпендикулярно оси z₂₃ и от полученной точки А₂₃ откладываем отрезок длиной y_A.

 

Проекции прямых линий

Положение прямой линии в пространстве вполне определяется двумя ее любыми точками. В общем случае проекцией прямой является прямая, в частном случае - точка, если прямая перпендикулярна плоскости проекций. Для построения проекций прямой достаточно иметь либо проекции двух ее точек, либо проекцию одной точки прямой и направление прямой в пространстве.

По своему расположению в пространстве относительно плоскостей проекций прямые линии разделяют на прямые общего положения, уровня и проецирующие.

2.2.1. Прямые общего положения. Это прямые, не параллельные и не перпендикулярные к плоскостям проекций. Проекции А₁В₁, А₂В₂ и А₃В₃ отрезка АВ прямой АВ общего положения (рис. 2.18, а) наклонены под острыми углами к осям x₁₂, y₁₃ и z₂₃. Длины проекций отрезков этой прямой всегда меньше самого отрезка. Трехкартинный комплексный чертеж отрезка прямой общего положения, построенный по двум точкам А и В, показан на рис.2.18, б.

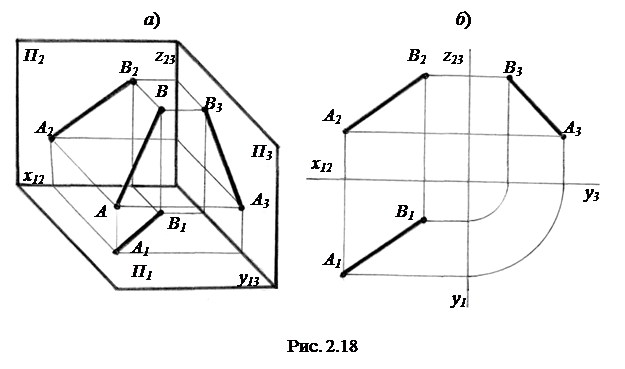
2.2.2. Прямые уровня. Это прямые, параллельные одной из плоскостей проекций - П₁, П₂ или П₃. Следовательно, имеем три вида прямых уровня:

1) горизонтальная уровня a (горизонталь), параллельная П₁ (прямая a с отрезком AB на ней на рис. 2.19, а, б);

2) фронтальная уровня (фронталь), параллельная П₂ (прямая b c отрезком CD на ней на рис. 2.20, а);

3) профильная уровня, параллельная П₃ (прямая с с отрезком ЕF на ней на рис. 2.20, б). На рис. 2.20 наглядные изображения прямых b и c относительно плоскостей проекций не показаны.

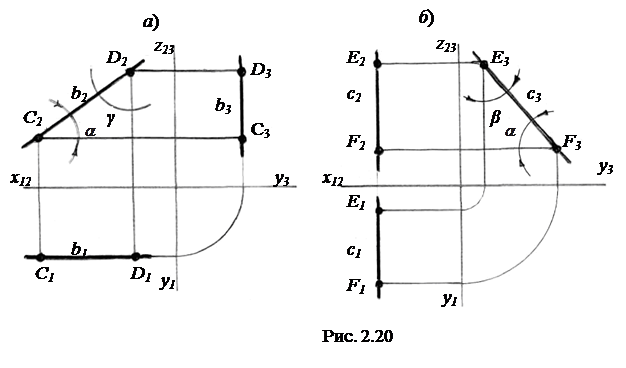Одноименные проекции отрезков прямых уровня проецируются в натуральную величину, а разноименные параллельны осям, отделяющим их от одноименных. При этом для горизонтали одноименная проекция - горизонтальная, а разноименные - фронтальная и профильная и т. п.

Углы наклона прямых уровня a, b и c к плоскостям проекций П₁, П₂ и П₃ принято обозначать соответственно α, β и γ (на рис. 2.19 углы α, β и γ не показаны).

2.2.3. Проецирующие прямые. Это прямые, перпендикулярные к одной из плоскостей проекций и параллельные двум другим. Следовательно, имеем три вида проецирующих прямых:

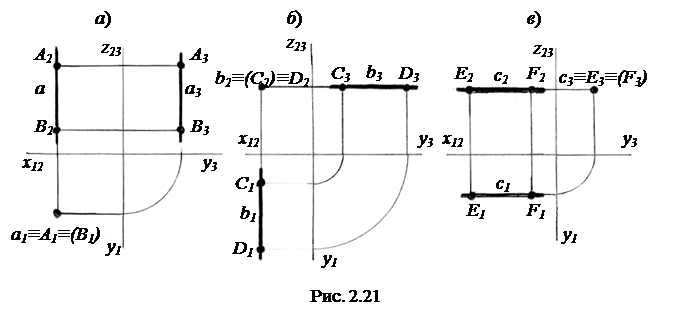
1) горизонтально-проецирующая прямая, перпендикулярная П₁ (прямая а с отрезком AB на ней на рис. 2.21, а);

2) фронтально-проецирующая прямая, перпендикулярная П₂ (прямая b с отрезком CD на ней на рис. 2.21, б);

3) профильно-проецирующая прямая, перпендикулярная П₃ (прямая c с отрезком EF на ней на рис. 2.21, в).

На рис. 2.21 в скобки заключены проекции невидимых точек. Вопрос определения видимости точек на проекциях подробнее будет рассмотрен ниже в п. «Скрещивающиеся прямые».

У проецирующих прямых одноименные проекции представляют собой точки, что вытекает из существа проецирующей прямой, вдоль которой ведется проецирование.

Каждая разноименная проекция проецирующей прямой перпендикулярна оси, отделяющей ее от одноименной проекции, а разноимённая проекция отрезка, расположенного на прямой уровня, является натуральной величиной этого отрезка.

2.2.4. Определение натуральной величины отрезка прямой общего положения. Натуральную величину прямой частного положения можно сразу определить на комплексном чертеже этой прямой.

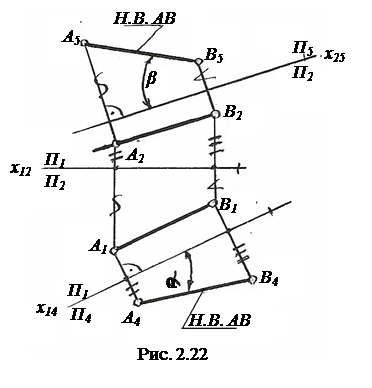Для определения натуральной величины отрезка прямой общего положения можно применить рассмотренный ранее (см. п. 2.1.2) способ замены плоскостей проекций. На рис.2.22 показано определение натуральной величины (Н.В.) отрезка AB прямой общего положения и определение углов наклона его к Π₁ (угол α) и к Π₂ (угол β) этим способом.

Дополнительная плоскость Π₄ проведена параллельно AB (х₁₄||A₁B₁). Прямая AB преобразована в положение фронтали, следовательно A₄B₄ – натуральная величина AB.

Проведя дополнительную плоскость Π₅||AB (х₂₅||A₂B₂), также можно определить натуральную величину AB. A₅B₅ – натуральная величина AB. Прямая AB в системе Π₂ - Π₅ стала горизонталью.

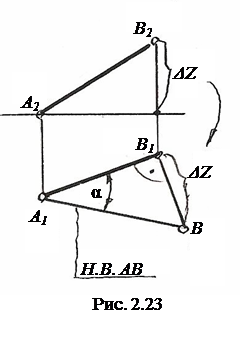На рис.2.23 показано определение натуральной величины AB методом треугольника. Натуральная величина отрезка равна гипотенузе прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – алгебраическая разность расстояний его концов от плоскости Π₁ (ΔZ).

2.2.5. Взаимное положение прямых. Прямые линии в пространстве могут быть параллельными, пересекаться и скрещиваться.

Параллельные прямые. Из свойств параллельных проекций следует, что если прямые в пространстве параллельны, то все три пары их одноименных проекций параллельны. Очевидно и обратное положение: если одноименные проекции прямых параллельны, то прямые в пространстве параллельны.

Пересекающиеся прямые. Две пересекающиеся прямые лежат в одной плоскости и имеют одну общую точку. Из свойств параллельных проекций известно, что если точка лежит на прямой, то ее проекции лежат на проекциях прямой. Если точка лежит и на той и на другой прямой, т. е. в точке пересечения прямых, то ее проекция должна лежать сразу на двух одноименных проекциях прямых, а следовательно, в точке пересечения проекций прямых.

Так, если отрезки AB и CD двух прямых пересекаются в точке K, то проекции отрезков A₁B₁ и C₁D₁ пересекаются в точке K₁, являющейся проекцией точки K (рис. 2.26, а). Поэтому, если одноименные проекции прямых пересекаются в точках, лежащих на одной линии проекционной связи, то прямые в пространстве пересекаются (рис. 2.26, б).

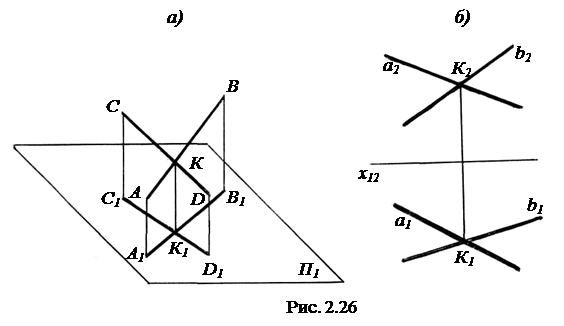
Для определения того, пересекаются прямые или нет, достаточно, чтобы это условие выполнялось для двух каких-либо проекций. Исключение составляет случай, когда одна из пересекающихся прямых является профильной уровня. В этом случае для проверки пересечения прямых необходимо построение профильной проекции.

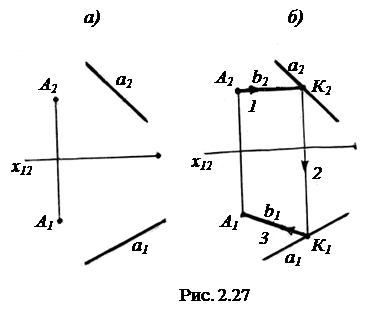
Пусть через точку A необходимо провести горизонталь b, пересекающую прямую a (рис. 2.27, а). Для этого через точку A₂ проводим b₂║ x₁₂ (этап 1) до пересечения с a₂ в точке K₂ (рис.2.27, б). Далее с помощью линии проекционной связи на a₁ находим точку K₁ (этап 2) и, соединяя точки A₁ и K₁ (этап 3), получаем b₁.

Скрещивающиеся прямые. Скрещивающиеся прямые a и b не лежат в одной плоскости и, следовательно, не параллельны и не имеют общих точек (рис.2.28, а). Поэтому, если прямые скрещивающиеся, то хотя бы одна пара их одноименных проекций не параллельна, и точки пересечения одноименных проекций не лежат на одной линии проекционной связи (рис. 2.28, б).

Каждая такая точка пересечения является проекцией двух точек, принадлежащих прямым; эти две точки лежат на одном проецирующем луче и называются конкурирующими.

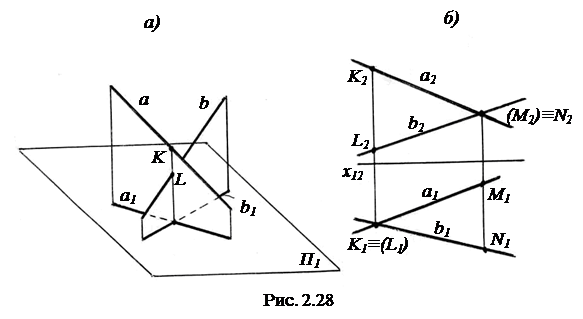
Точки K и L (рис. 2.28, а) лежат на одном горизонтально-проецирующем луче. Горизонтальные проекции точек совпадают и находятся в точке пересечения горизонтальных проекций a₁ и b₁ прямых. Точка K a, точка L b. Видно, что точка K выше точки L. Считают, что при проецировании на П₁ точка K видна, а точка L - не видна (закрыта от наблюдателя точкой К).

Точки M и N лежат на одном фронтально-проецирующем луче (рис. 2.28, б). Фронтальные проекции точек совпадают и находятся в точке пересечения фронтальных проекций прямых a₂ и b₂. Точка M a, точка N b. Точка N дальше от П₂, чем точка M, т. е. ближе к глазам наблюдателя, и поэтому при проецировании на П₂ точка N видна, а точка M - не видна. Обозначения проекций невидимых точек принято заключать в круглые скобки.