Комплексный двухкартинный чертеж точки. 2 страница

Проекции кривых линий

Кривые линии могут быть плоскими и пространственными. Они могут быть заданы аналитически с помощью уравнений и графически с помощью чертежа. В начертательной геометрии кривые линии задают с помощью чертежа.

Для построения проекций кривых линий необходимо знать приемы построения некоторых локальных характеристик: радиуса и центра кривизны, касательной, нормали и др.

2.3.1. Плоские кривые линии. Плоскими называются кривые линии, все точки которых принадлежат одной единственной плоскости. Искривленность кривой характеризуется радиусом кривизны или кривизной.

Окружность, соприкасающаяся с кривой а в данной точке M (рис. 2.29) проходит через точку M и бесконечно близкие от нее точки M¹ и M². Радиус этой окружности называется радиусом кривизны, а центр ее - центром кривизны. Кривизной (К) называется величина, обратная радиусу, т. е. K= 1/ R.

Касательной в данной точке M к кривой a (рис. 2.30) называется предельное положение секущей прямой, проведенной через точку M, когда ее длина становится равной нулю. На рис. 2.30 проведена секущая

MM¹. Пусть точка M¹ двигается вдоль кривой по направлению к точке M. В момент совпадения точек M¹ и M секущая

становится касательной.

Нормалью в данной точке M называется прямая, перпендикулярная к касательной.

Центр кривизны (центр соприкасающейся окружности) всегда лежит на нормали. Касательная как с плоской, так и с пространственной кривой имеет одну точку соприкосновения. Следовательно, проекция касательной к пространственной кривой будет касательной к проекции кривой, так как будет иметь с проекцией кривой только одну точку соприкосновения.

Рассмотрим практические способы построения касательных к плоским изображениям кривых, которые также могут быть проекциями пространственных кривых.

Построение касательной с помощью зеркальца. К изображению кривой в данной точке ребром приставляют зеркальце. Ставят его поперек кривой и поворачивают его до тех пор, когда отражение кривой и сама кривая будут представлять собой плавную, без изломов линию. В этот момент ребро зеркальца направлено точно по нормали. Касательная будет к ней перпендикулярна.

Построение касательной с помощью кривой ошибок. Кривой ошибок называется кривая линия, каждая точка которой строится по некоторому правилу. Только одна точка кривой ошибок отвечает необходимому условию. Все остальные точки являются ошибками.

Пусть, например, через точку K требуется провести касательную t к кривой l (рис.2.31). Для этого выполняем следующие действия:

1) Через точку K проводим несколько секущих AB (A¹B¹, A²B² и A³B³) и каждую делим пополам, обозначив середины секущих буквой C (C¹, C² и C³).

2) Соединяем точки C¹, C² и C³ плавной кривой и получаем кривую ошибок m. Продолжаем m до пересечения с заданной кривой l в точке M. В точке касания длина секущей равна нулю и ее середина совпадает с точкой касания. Поэтому считаем, что точка M пересечения кривой ошибок m с заданной кривой l и есть точка касания.

3) Точку K соединяем с M и получаем касательную t.

Пусть через точку M кривой l необходимо построить касательную t и нормаль n (рис. 2.32).

Последовательность построений в этом случае будет следующая:

1) В произвольном месте чертежа проводим прямую i примерно перпендикулярно будущей касательной.

2) Через точку M проводим ряд секущих a, b, c с одной и d, e, f с другой стороны от точки M, продолжая их до пересечения с прямой i.

3) От точек A, B, C пересечения секущих a, b, c с прямой i вдоль их откладываем длины секущих MA¹, MB¹, и MC¹ слева от прямой i и получаем точки A², B² и C². Для секущих d, e, f длины MD¹, ME¹ и MF¹ откладываем справа от прямой i и получаем точки D², E² и F².

4) Точки A², B², C², …, F² соединяем плавной кривой и получаем кривую ошибок m, которая пересекается с прямой i в точке K.

5) Соединяем точку M с точкой K прямой t, которая является секущей нулевой длины, т. е. касательной к заданной кривой l в точке M.

6) Через точку M перпендикулярно касательной t проводим нормаль n.

2.3.2. Пространственные кривые линии. Пространственные кривые линии имеют двоякую кривизну. Все точки пространственной кривой не лежат в одной плоскости. Ознакомимся, в качестве примера, с цилиндрической винтовой линией, которая имеет большое применение в технике.

Цилиндрическая винтовая линия располагается на поверхности прямого кругового цилиндра. Она образуется при сложном движении точки. Точка движется равномерно и прямолинейно вдоль образующей цилиндра и равномерно вращается вместе с образующей вокруг оси цилиндра.

Винтовая линия называется правой, если при своем поступательном движении от наблюдателя точка вращается по ходу часовой стрелки, и левой, если против хода часовой стрелки. Построение проекций цилиндрической винтовой линии дано на рис. 2.33.

Пусть имеется цилиндр диаметром d, с осью i. Наметим 12 образующих цилиндра, расположенных на равных расстояниях от друг друга. Будем считать, что образующая, переходя из одного положения в другое, равномерно вращается вокруг оси i. Вверх вдоль образующей движется точка. При повороте образующей на 1/12 оборота точка перемещается вверх на 1/12 шага h. Шагом винтовой линии называется величина перемещения точки параллельно оси при ее повороте на один полный оборот.

Соединяя последовательно фронтальные проекции полученных точек, строим фронтальную проекцию винтовой линии, которая представляет собой синусоиду.

Горизонтальной проекцией винтовой линии является окружность. Если развернуть цилиндрическую поверхность вместе с нанесенной на нее винтовой линией, то вращательное движение образующей на развертке превращается в ее поступательное движение вдоль развернутой окружности основания цилиндра.

В результате сложения двух равномерных поступательных движений вдоль развернутой окружности вправо и вдоль образующей вверх образуется прямая линия. Угол наклона развернутой винтовой линии к основанию:

Ψ= arctg ,

где h - шаг винтовой линии; d - диаметр образующего цилиндра.

Угол Ψ называется углом наклона винтовой линии. Если навернуть винтовую линию обратно на цилиндр, то касательные в каждой точке винтовой линии наклонены к плоскости основания цилиндра под постоянным углом Ψ.

Построим касательную к винтовой линии в точке M. Как было показано выше, проекция касательной к кривой линии касательна к проекции этой кривой.

Возьмем некоторую точку M, принадлежащую винтовой линии и заданной проекциями M₁ и M₂, и проведем через нее касательную к винтовой линии.

Горизонтальная проекция касательной к винтовой линии будет касательна к окружности, в которую она проецируется на П₁, и перпендикулярна радиусу i₁M₁. При построении касательной к фронтальной проекции винтовой линии используем свойство одинакового наклона всех касательных.

Отметим на развертке винтовой линии точку M¹, соответствующую пространственной точке M, лежащей на винтовой линии. Из M¹ опускаем перпендикуляр к развернутому основанию цилиндра и получаем точку M². При этом отрезок основания O¹M² равен дуге окружности, на которую опирается часть винтовой линии от ее начала до точки M. Отрезок O¹M² называется подкасательной.

Из горизонтальной проекции M₁ проводим касательную к окружности и откладываем на ней отрезок, равный подкасательной O¹M², и получим точку A₁ - основание касательной. Точка A₁ лежит на плоскости П₁, т. к. A П₁. Фронтальная проекция A₂ этой точки лежит на оси x₁₂. Фронтальная проекция касательной проходит через проекции A₂ и M₂.

Можно представить себе винтовую линию и на других поверхностях, например на конической поверхности, на сфере и т. д. Если вращать образующую конической поверхности и перемещать вдоль нее точку, то образуется коническая винтовая линия. Если вращать окружность вокруг своей оси и вдоль нее перемещать точку, то образуется сферическая винтовая линия.

Проекции поверхностей. Задание поверхности на чертеже

Поверхностью в геометрии называется граница, отделяющая геометрическое тело (цилиндр, конус, шар и т.д.) от внешнего пространства. На чертежах (эпюрах) изображают только точки и линии (прямые или кривые). Поэтому поверхность можно изобразить только тогда, когда она проецируется в линию или совокупность линий.

Поверхность может быть задана с помощью модели (обувная колодка, манекен и др.), с помощью уравнения, кинематически – как след движущейся в пространстве линии, и др. В начертательной геометрии принят кинематический способ образования поверхности. Можно сказать, что поверхность – это непрерывная совокупность последовательных положений движущейся в пространстве прямой или кривой линии. Линия, которая при своем движении образует поверхность, называется образующей.

2.4.1. Задание поверхности с помощью определителя. Для того, чтобы задать поверхность, достаточно задать образующую поверхности и определить закон, по которому она перемещается в пространстве. Законы движения образующих могут задаваться различно:

1) Образующая движется, пересекая какую-либо неподвижную линию, которая называется направляющей.

2) Образующая движется, пересекая две или три направляющие линии.

3) Образующая движется параллельно самой себе или параллельно некоторой плоскости, которая называется плоскостью параллелизма и др.

Образующая вместе с геометрическими фигурами, определяющими ее движение, а также закон ее движения составляют определитель поверхности. Можно сказать, что определитель поверхности представляет собой совокупность независимых параметров, однозначно задающих поверхность.

Определитель состоит из двух частей:

1) Геометрическая часть – фигуры (точки, линии, поверхности) подвижные и неподвижные, с помощью которых образуется поверхность.

2) Алгоритмическая часть – правило движения (закон движения) образующей по отношению к неподвижным фигурам определителя.

В ряде случаев образующая при своем движении может деформироваться, что тоже оговаривается в алгоритмической части определителя. Основанием к составлению определителя является анализ способа образования поверхности и ее основных свойств. Каждая поверхность может быть задана разными определителями.

Для примера рассмотрим определитель произвольной цилиндрической поверхности (рис. 2.34). Запись определителя имеет вид:

Ф (l, a) - цилиндрическая поверхность

(геометрическая часть) (алгоритмическая часть)

Эта запись дается совместно с чертежом. В записи геометрической части буквой Ф обозначается поверхность, буквой l – образующая, буквой а - направляющая. Форма и положение в пространстве образующей и направляющей определяются по чертежу.

В записи алгоритми-ческой части дается название поверхности. Для поверх-ности с данным названием общеизвестно, какое движе-ние совершает l, образуя поверхность Ф. Но можно и подробно записать характер движения образующей. В нашем случае образующая l движется параллельно самой себе и все время пересекает направляющую а. Определитель вполне определяет поверхность, т.к. с его помощью можно построить ее проекции.

На рис. 2.35, а задан комплексный чертеж определителя цилиндрической поверхности Ф (l, a) и проекция А₂ точки А, принадлежащей поверхности. Необходимо построить горизонтальную проекцию А₁ точки А.

Зная алгоритмическую часть определителя, выполним следующие построения (рис. 2.35, б):

1) Через А₂ параллельно l₂ проводим и находим фронтальную проекцию В₂ точки пересечения с а₂ (этап 1). Этапы указаны стрелками.

2) С помощью линии проекционной связи на а₁ находим В₁ (этап 2).

3) Через точку В₁ проводим параллельно l₁ (этап 3).

4) На с помощью линии связи строим А₁ (этап 4).

2.4.2. Каркас поверхности. Если построить некоторое количество образующих по описанному в алгоритме определителя способу, то получим каркас или сеть поверхности (рис. 2.36).

Изображенный на рис. 2.36, а каркас называется однопараметрическим, т.к. он состоит из линий, принадлежащих одному семейству. Это дискретный каркас, он состоит из конечного числа линий.

Можно представить себе и непрерывный каркас образующих. Непрерывный каркас – это множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит только одна линия каркаса.

На одной и той же поверхности, в зависимости от определителя, можно представить себе и другие каркасы. Если в определителе цилиндрической поверхности образующую и направляющую поменять местами и считать, что кривая а будет образующей, которая движется параллельно самой себе и все время пересекает направляющую l, то получится другой однопараметрический каркас (рис. 2.36, б).

Если на поверхности построить два каркаса, то получится двупараметрический каркас (рис. 2.36, в). Через каждую точку поверхности, заданной двупараметрическим каркасом, проходят две линии каркаса.

2.4.3. Задание поверхности, не имеющей определителя. Существуют незакономерные поверхности, к которым относятся манекен, обувная колодка, кузова автомобилей, фюзеляжи самолетов, корпуса морских и речных судов, рельеф земной поверхности и др. Такие поверхности называются графическими и задаются дискретным каркасом. Чаще всего линии этого каркаса представляют собой плоские кривые, параллельные какой-либо плоскости проекций. Если плоскости линий каркаса параллельны горизонтальной плоскости проекций, то такие линии называются горизонтальными.

2.4.4. Очерк поверхности. Линия пересечения проецирующей поверхности, огибающей заданную поверхность, с плоскостью проекций называется очерком поверхности. На рис. 2.37 показано проецирование сферы Т на плоскость П₁. Множество горизонтально-проецирующих лучей, касательных к поверхности сферы, образуют огибающую горизонтально–проецирующую цилиндрическую поверхность Ф. Линия пересечения Ф и П₁ представляет собой горизонтальный очерк поверхности – окружность а₁.

Очерковой линией повер-хности называется линия, по которой огибающая проеци-рующая поверхность касается данной поверхности. В нашем случае очерковой линией будет большая окружность сферы а (экватор).

Изображения поверхнос-тей, заданных определителем, не всегда наглядны. Более наглядны изображения поверхностей с помощью очерков. Очерк поверхности почти всегда включает в себя ее определитель. При построении проекций точки, лежащей на поверхности, изображенной очерком, необходимо сначала выделить проекции определителя, а потом, пользуясь алгоритмом определителя, построить проекции точки.

На рис. 2.38, а поверхность наклонного эллиптического цилиндра задана определителем, а на рис. 2.38, б очерком. Горизонтальный очерк представляет собой линию, состоящую из отрезков прямых и кривых ; фронтальный очерк представляет собой параллелограмм .

Образующие горизонтального очерка и и образующие фронтального очерка и не совпадают друг с другом. Из проекций очерка можно выделить геометрическую часть определителя, которая будет состоять из эллипса и какой-нибудь образующей, например .

2.4.5. Проекции плоскостей. Плоскость можно рассматривать как частный случай поверхности. Плоскость Σ может быть образована за счет движения прямолинейной образующей l параллельно самой себе, при этом образующая пересекает все точки направляющей прямой а (рис. 2.39). Определитель плоскости в этом случае имеет вид: Σ (а, l).

Из геометрии известно, что плоскости вполне определяются:

1) Тремя точками А, В и С, не лежащими на одной прямой (рис.2.40, а).

2) Прямой а и точкой А вне её (рис. 2.40, б).

3) Двумя параллельными прямыми а и b (рис. 2.40, в).

4) Двумя пересекающимися прямыми а и b (рис. 2.40, г).

Задание плоскости пересекающимися прямыми а и b (рис. 2.40, г) можно рассматривать, как универсальный способ задания плоскости, так как все остальные можно привести к нему. Так, например, если плоскость задана тремя точками А, В и С (рис. 2.40, а), то, соединяя точки А с В и В с С, получаем пересекающиеся прямые АВ и ВС.

2.4.6. Виды плоскостей по их расположению в пространстве. По расположению относительно плоскостей проекций плоскости можно разбить на три вида:

1) плоскости общего положения – плоскости, не параллельные и не перпендикулярные плоскостям проекций;

2) плоскости проецирующие – плоскости, перпендикулярные к какой-либо плоскости проекций;

3) плоскости уровня – плоскости, параллельные какой-либо одной плоскости проекций и перпендикулярные двум другим.

Рассмотрим некоторые особенности каждого из перечисленных видов плоскостей.

Плоскости общего положения. На рис. 2.40 изображены плоскости общего положения. Для этих плоскостей характерно, что задающие их элементы (точки, прямые и др.) ни на одной проекции не сливаются в прямую линию, т.е. не лежат на одной прямой.

На рис. 2.41 задана плоскость Σ (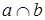) и одна проекция А₂ точки А, принадлежащей плоскости Σ. Будем считать, что а – направляющая, а b - образующая плоскости Σ. Помня, что все образующие параллельны между собой и все пересекаются с направляющей, выполним следующие построения:

1) Через точку А₂ проведем проекцию образующей m₂ ║ b₂ и построим точку К₂ пересечения m₂ с а₂ (этап 1).

2) На линии связи и на а₁ находим К₁ (этап 2).

3) Через К₁ проводим m₁ ║ b₁ (этап 3).

4) С помощью линии связи на m₁ находим А₁ (этап 4).

В данном построении образующая m₁, лежащая в плоскости Σ, строилась по точке и известному направлению. Однако при построении точки, лежащей в плоскости, можно воспользоваться не только образующей, лежащей в плоскости. На рис. 2.42 горизонтальная проекция точки А построена с помощью произвольной прямой. При этом выполнены построения:

1) Через заданную проекцию А₂ проводим произвольную прямую m₂ и, считая, что m лежит в плоскости Σ (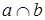), отмечаем точки ее пересечения К₂ и М₂ с а₂ и b₂ (этап 1).

2) Строим К₁ и М₁ на а₁ и b₁ с помощью линий связи (этап 2).

3) Соединим К₁ и М₁ и получим m₁ (этап 3).

4) На m₁ с помощью линии связи находим А₁ (этап 4).

Очевидно, для того, чтобы в плоскости построить точку, необходимо в этой плоскости провести прямую и затем на прямой взять точку. При этом прямая расположена в плоскости, если она проходит через две точки, принадлежащие плоскости.

Проецирующие плоскости. Различают три вида проецирующих плоскостей:

1) Горизонтально-проецирующие, перпендикулярные П₁.

2) Фронтально-проецирующие, перпендикулярные П₂.

3) Профильно-проецирующие, перпендикулярные П₃.

При изображении проецирующих плоскостей надо иметь в виду, что одноименная проекция такой плоскости всегда вырождается в прямую, как было показано ранее. Эта прямая называется главной проекцией или следом проецирующей плоскости; эту проекцию также называют вырожденной. Для того, чтобы отличать проецирующую плоскость от прямой, главную проекцию проецирующей плоскости на чертеже часто изображают с утолщением конца.

На рис. 2.43, а показано наглядное изображение произвольной горизонтально-проецирующей плоскости Σ (а ║ b) и ее главной проекции Σ₁. Комплексный чертеж этой плоскости приведен на рис.2.43, б. На главную проекцию плоскости проецируются все точки, лежащие в плоскости.

Фронтально-проецирующая плоскость Т (с d) изображена на рис. 2.44, а, профильно-проецирующая плоскость Г (е f) - на рис. 2.44, б и профильно-проецирующая плоскость Р (а ║ b) - на рис. 2.44, в.

Благодаря проецирующему свойству прое цирующие плоскости можно задавать одной своей главной проекцией (следом, вырожденной проекцией). На рис. 2.45 задана фронтально-проецирующая плоскость Σ.

Из стереометрии известно, что плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой. Поэтому в каждой проецирующей плоскости можно построить одноименную проецирующую прямую. На рис. 2.43, б в плоскости Σ (а ║ b) построена горизонтально-проецирующая прямая с. На рис. 2.44, а в плоскости Т (с d) построена фронтально-проецирующая прямая f.

В плоскостях Г (е f) (рис. 2.44, б) и Р (а ║ b) (рис. 2.44, в) есть прямые, перпендикулярные П₃. Следовательно, эти плоскости являются профильно-проецирующими. Таким образом, профильно-проецирующие плоскости можно задавать только проекциями на П₁ и П₂.

Вопрос о принадлежности точки и прямой к проецирующей плоскости решается проще, чем у плоскости общего положения. Проекция точки или прямой всегда находится в главной проекции плоскости, выродившейся в линию. Так, на рис.2.46, а показаны проекции точки А, а на рис. 2.46, б - прямой а, принадлежащих соответственно горизонтально- проецирующей плоскости Σ и фронтально-проецирующей плоскости Т.

Плоскости уровня. Различают три вида плоскостей уровня: