Свойства параллельных проекций.

МИНИСТЕРСТВО ОБРАЗОВАНИя И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ДИЗАЙНА И ТЕХНОЛОГИИ»

(ФГБОУ ВПО «МГУДТ»)

 

Никифоров В.М., Фатеев В.И.

 

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

 

Ч а с т ь 1

 

ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ФИГУР

И ОСНОВЫ ПОСТРОЕНИЯ ТЕХНИЧЕСКОГО РИСУНКА

 

Учебное пособие

 

Допущено к изданию редакционно-издательским советом университета

в качестве учебного пособия для подготовки бакалавров

по направлению 54.03.01 Дизайн

 

 

 

 

М о с к в а

М Г У Д Т

2 0 1 4

 

УДК 514.18(072)

H62

 

Н62 Никифоров В.М., Фатеев В.И. Начертательная геометрия. Часть 1. Ортогональные проекции геометрических фигур и основы построения технического рисунка: Учебное пособие. – 2-е изд., перераб. и доп. -М.: МГУДТ, 2014. –101с.

 

Рецензенты:

- доцент кафедры стандартизации и инженерно-компьютерной графики ФГБОУ ВПО «Российский химико-технологический университет им.Д.И. Менделеева», к.т.н. Киракосян В.Р.;

- доцент кафедры начертательной геометрии, инженерной и компьютерной графики ФГБОУ ВПО «МГУДТ», к.т.н. Баринов Н.В.

 

 

Часть 1 учебного пособия содержит следующие разделы курса начертательной геометрии: ортогональные проекции точки, прямой и кривой линии, плоскости и разнообразных поверхностей; позиционные задачи; аксонометрические проекции; теория теней. Эти разделы являются теоретической основой для построения технических рисунков геометрических объектов и их комбинаций.

Во втором издании учтены последние изменения и дополнения в соответствущих рабочих программах учебных дисциплин.

Учебное пособие предназначено для обучающихся по направлению подготовки 54.03.01 Дизайн очной формы обучения и будет использовано при изучении дисциплины «Технический рисунок».

 

УДК 514.18(072)

 

Подготовлено к печати на кафедре начертательной геометрии, инженерной и компьютерной графики.

 

Печатается в авторской редакции.

 

ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ

 

1. Точки - A, B, C, … или 1, 2, 3, … (латинские прописные буквы или арабские цифры).

2. Прямые и кривые линии - a, b, c, … (строчные буквы латинского алфавита).

Отрезок прямой, ограниченный точками А и В – АВ.

3. Поверхности и плоскости - Σ, Δ, Τ, … (прописные буквы греческого алфавита).

4. Плоскости проекций – Π₁ (горизонтальная), Π₂ (фронтальная), Π₃ (профильная). Новая плоскость при замене плоскостей проекций – буквой Π с добавлением подстрочного индекса (Π₄, Π₅, Π₆ … - в методе ортогонального проецирования; Π_A – плоскость аксонометрических проекций).

5. Проекции точек, прямых и поверхностей – той же буквой с добавлением подстрочного индекса, соответсвующего плоскости проекций, например А₁ – проекция точки А на плоскость П₁.

6. Обозначения проекций невидимых точек заключают в скобки, например (A₁), (B₂), (C₃).

7. Углы - α, β, γ, … (строчные буквы греческого алфавита). Прямой угол обозначается точкой внутри сектора:

8. Основные операции:

8.1. ≡ - совпадение двух геометрических фигур, например Σ_n≡Σ_K – фигуры Σ_n и Σ_K совпадают.

8.2.׀׀ – параллельны.

8.3. ╫ – не параллельны.

8.4. – перпендикулярны.

8.5. 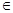– принадлежит, является элементом.

8.6. 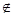– не принадлежит, не является элементом.

8.7. – пересечение фигур.

8.8. Σ_n Σ_K – фигура Σ_n есть подмножество фигуры Σ_K.

8.9. Σ_n Σ_K – фигура Σ_n не является подмножеством фигуры Σ_K.

8.10. = - равенство величин, например АВ=CD - отрезки АВ и CD равны по длине; результат геометрической операции, например К = а b – точка К является результатом пересечения прямых а и b.

7. Оси проекций и оси координат - x, y, z. Оси с индексами указывают на соответствующие плоскости проекций. Так, ось x₁₂ разделяет поле горизонтальных проекций (индекс 1) и поле фронтальных проекций (индекс 2).

Значения координат точек обозначаются буквами, соответствующими осям координат, с добавлением подстрочного индекса, соответствующего точке, например x_В, y_В, z_B - координаты точки В).

8. Последовательность геометрических фигур – надстрочным индексом (точек – A¹, A², A³ …; прямых - а¹, а², а³ … и т. д.).

9. Аксонометрические проекции точек, прямых, координатных осей - буквами, соответствующими натуре, с добавлением подстрочного индекса «А» (А_А – аксонометрическая проекция точки А; а_А – аксонометрическая проекция прямой а; x_A, y_A, z_A – аксонометрические проекции осей координат x, y, z). Часто с целью упрощения индекс«А» опускается.

10. Проекции тени от точки и прямой в аксонометрии и в перспективе – буквами, соответствующими натуре, с добавлением подстрочного индекса «0» (A₀ и a ₀ – соответственно проекции тени от точки A и прямой a).

 

В В Е Д Е Н И Е

 

Начертательная геометрия является одной из первых фундаментальных дисциплин, изучаемых студентами, обучающимися по направлению подготовки бакалавров 54.03.01 Дизайн, как и студентами многих других направлений подготовки специалистов. Она представляет собой раздел проекционной геометрии, в котором изучаются способы изображения пространственных геометрических объектов на плоскости, а также способы решения позиционных, метрических и конструкторских задач. При этом построение различного рода геометрических фигур на плоскости или, иными словами, выполнение на листе бумаги изображений (рисунков), отвечающих заданным условиям, является, в основном, содержанием работы дизайнеров, как будущих специалистов.

Неизмеримо возросший уровень требований к качеству подготовки бакалавров, магистров и специалистов выводит начертательную геометрию в ряд основных дисциплин. Таким образом начертательная геометрия относится к дисциплинам, с помощью которых осуществляется подготовка выпускников вузов, владеющих способами графических построений изображений объектов различной геометрической формы.

Начертательная геометрия со времён её основоположника Г. Монжа (1746-1818гг) заняла достойное место в высшей школе как наука, без которой невозможно формирование будущего специалиста. Важнейшее прикладное значение этой дисциплины состоит в том, что она учит грамотно владеть общедоступным выразительным технологическим языком – языком чертежа и рисунка, выполнять построение рисунка объекта, а также выполнять чертежи и свободно их читать.

Современное производство и дизайн-проектирование невозможно представить без применения чертежей и рисунков. При этом чертёж – изображение объекта на плоскости, по которому можно судить о его форме, назначении и размерах. Чертёж и рисунок являются средствами выражения мысли технолога, конструктора, дизайнера и др. и представляют собой одни из важнейших проектно-конструкторских документов.

Изучение начертательной геометрии значительно развивает пространственное воображение и способствует развитию навыков правильного логического мышления. Более того, совершенствуя способность по плоскому изображению мысленно создавать представление о форме геометрического объекта, начертательная геометрия готовит будущего специалиста к успешному изучению как общепрофессиональных, так и специальных дисциплин – «Рисунок», «Проектная графика», «Проектирование в графическом дизайне», «Дизайн и рекламные технологии», «Основы теории и методологии проектирования в промышленном дизайне» и др.

Незримая работа мысли над вынашиванием дизайнерской идеи будет тем плодотворнее, чем сильнее развито пространственное воображение, и чем свободнее владеет специалист способами изображения пространственных геометрических объектов на плоскости.

Основной задачей учебного пособия «Начертательная геометрия» является изучение теоретических основ построения изображений объектов дизайна - ландшафта, интерьера, костюма, аксессуаров, промышленных изделий и др. Изображение любого объекта может быть выполнено в виде аксонометрической проекции или в перспективе. Так как современное дизайн-проектирование немыслимо без выполнения в проектной документации наглядных изображений объектов проектирования, то в соответствующих разделах пособия рассматриваются вопросы построения технических рисунков этих объектов в виде аксонометрии. Для получения изображений с большей наглядностью в пособии дана теория теней и рассмотрены способы построения собственной и падающей тени на этих изображениях.

Принято считать, что технический рисунок – наглядное изображение предмета, выполненное, как правило, в прямоугольной аксонометрии (иногда в косоугольной) с применением чертёжных инструментов и от руки для технико-технологических, производственных и рекламных целей. Для большей наглядности изображений объектов в дизайн-проектировании в настоящее время технический рисунок выполняют с дополнительными построениями собственной тени и падающей тени на опорную поверхность и рядом стоящие предметы при любом способе освещения.

Учебное пособие разработано с учётом многолетнего опыта учебной, методической и научной работы авторов в Московском государственном университете дизайна и технологии (МГУДТ). Большую помощь в разработке структуры учебного пособия и последовательности изложения разделов оказал профессор Э. Х. Фридлянд, за что авторы выражают ему огромную благодарность.

МЕТОД ПРОЕКЦИЙ

 

Основные понятия и определения

 

Методом проекций в начертательной геометрии называют способ, посредством которого получают изображения геометрических фигур. При этом начертательная геометрия рассматривает лишь их геометрические свойства.

1.1.1. Геометрические фигуры. К геометрическим фигурам, подлежащим изучению, относятся абстрактные точки, прямые и кривые линии, поверхности и геометрические тела.

Точка представляет собой абстрактное понятие, не имеющее измерений. Можно говорить только о положении точки в пространстве.

Линия (прямая или кривая) состоит из множества точек, не имеет толщины и имеет лишь одно измерение. Можно говорить о положении линии в пространстве и о ее длине.

Поверхность (плоскость, цилиндрическая и коническая поверхности, сфера и др.) представляет собой множество точек или множество линий, не имеет толщины и имеет два измерения вдоль поверхности. Можно говорить о положении поверхности в пространстве и ее размерах.

Пространственные геометрические тела могут быть ограничены точками, линиями и поверхностями.

В конечном счете каждое геометрическое тело (точнее, поверхность, ограничивающая тело) может быть представлено множеством точек.

Поэтому, прежде чем перейти к изображению пространственных тел, изучим законы изображений с помощью точки.

1.1.2. Элементы и особенности метода проекций. Процесс проецирования заключается в проведении через выбранную точку А изображаемой геометрической фигуры проецирующего луча i (прямая линия) до пересечения в точке А_N с некоторой плоскостью проекций П_N. Точка А_N является проекцией (изображением) точки А на плоскости П_N (рис. 1.1).

Таким образом, имеем четыре элемента метода проекций: пространственая точка - А; проецирующий луч - i; плоскость проекций (картинная плоскость, плоскость изображений) - П_N ; проекция точки (изображение точки) – А_N , (обозначается той же буквой, что и пространственная точка, но с индексом плоскости проекций). Операция получения проекции точки называется проецированием.

Из рис. 1.1 вытекают две особенности метода проекций.

Первая особенность заключается в том, что каждой пространственной точке А¹, А², А³, расположенной на данном проецирующем луче i, соответствует только одна точка А_N плоскости проекций П_N , т. е.

.

С другой стороны, каждой точке А_N плоскости проекций П_N соответствует бесчисленное множество точек А¹, А², А³, …, расположенных на проецирующем луче i, проходящем через данную точку А_N , т. е.

А_N→ Аⁿ i.

Эти особенности наглядны и не нуждаются в специальном доказательстве.

Из второй особенности вытекает, что одной проекции точки недостаточна для определения положения самой точки в пространстве. Можно сказать, что изображение точки на одной плоскости проекций является неполным. По одному изображению невозможно представить себе место расположения точки в пространстве.

Ниже мы познакомимся со способами получения полных изображений точки, по которым можно будет определить ее положение в пространстве.

Точки, расположенные на одном проецирующем луче, называются конкурирующими.

Системы проецирования

 

Определяющим в той или иной системе проецирования является направление проецирующих лучей по отношению к плоскости проекций.

Рассмотрим наиболее распространенные центральную и параллельную системы проецирования.

1.2.1. Центральная система проецирования. Эту систему называют также конической, полярной или перспективной. В этой системе пространственные точки A, B и C, лежащие на кривой линии (рис. 1.2), проецируются на плоскость проекций П_N лучами i, j и k, проходящими через одну и ту же некоторую неподвижно взятую в пространстве точку P, которая называется центром или полюсом проекций.

Если спроецировать все точки кривой АВС, то фигура, составленная из множества проецирующих лучей, будет представлять собой коническую поверхность.

1.2.2. Параллельная система проецирования. Эта система проецирования является частным случаем центральной системы, когда полюс проекций отнесен в бесконечность.

В зависимости от направления проецирующих лучей относительно плоскости проекций параллельная система проецирования разделяется на косоугольную и ортогональную (прямоугольную).

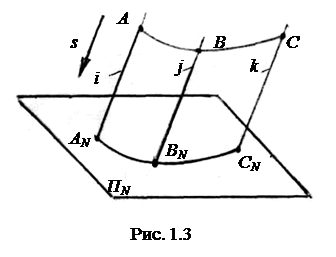
В косоугольной системе проецирования проецирующие лучи i, j и k направлены к плоскости проекций П_N под острым углом (рис. 1.3) и параллельны некоторому заданному направлению s.

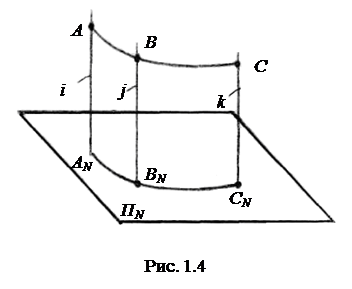
В ортогональной (прямоугольной) системе проецирования проецирующие лучи i, j, k направлены перпендикулярно плоскости проекций П_N (рис. 1.4). Поэтому можно сказать, что ортогональной проекцией точки называется основание перпендикуляра, опущенного из точки на плоскость проекций.

 

1.2.3. Свойства изображений. Изображения, полученные при помощи рассмотренных выше систем, обладают различными свойствами. К свойствам изображений относят их наглядность и точность.

Наглядность - свойство изображения передавать предметы так, как их видит человеческий глаз в действительности.

Точность - свойство изображения, дающее возможность правильно представить себе размеры, взаимное положение частей и форму предмета.

Изображения, полученные при помощи центральной системы проецирования, обладают большой наглядностью, но не точны. Центральная система проецирования применяется главным образом в живописи и архитектуре, при построении перспективы художниками-дизайнерами.

На рис. 1.5 выполнено изображение с помощью центрального проецирования. Чертеж нагляден, читателю кажется, что дорога одинаковой

ширины уходит в даль, и около дороги стоят столбы равной высоты, но чертеж не точен, так как на изображении ширина дороги и высота столбов не постоянны, и их затруднительно измерить.

Наглядность перспективных изображений обусловлена тем, что ход лучей в перспективе сходен с ходом лучей, изображающих предмет на сетчатке глаза. Центр хрусталика глаза является полюсом проекций, а сетчатка глаза – плоскостью проекций (рис. 1.6).

Изображения, выполненные в косоугольных параллельных проекциях, менее наглядны, но более точны; кроме того, они проще по выполнению. Почти все наглядные изображения, иллюстрирующие данное учебное пособие, выполнены по законам параллельных косоугольных проекций (использована косоугольная фронтальная изометрическая проекция, см. далее п.4.3.2).

Прямоугольные проекции не обладают наглядностью, зато они точны и измеримы. С их помощью можно решать различные пространственные геометрические задачи, пользуясь только линейкой и циркулем. Прямоугольная система проецирования является основой для выполнения инженерных чертежей, по которым изготовляются изделия.

Свойства параллельных проекций.

Рассмотрим некоторые свойства параллельных проекций.

Точка в натуре проецируется в точку на плоскость проекций. Это свойство вытекает из правил построения в методе проекций.

Прямая в натуре, в общем случае, проецируется в прямую на плоскость проекций. Если прямая направлена вдоль проецирующего луча, то ее проекцией будет точка.

Для того, чтобы спроецировать прямую, необходимо взять все ее точки и каждую спроецировать на плоскость проекций. Множество полученных проекций точек будет представлять собой проекцию прямой.

Возьмем на прямой АВ (рис. 1.7) точки С¹, С² и С³ и спроецируем их на плоскость П_N параллельно некоторому заданному направлению. Образовавшееся множество лучей представляет собой плоскость, так как все лучи пересекают прямую АВ и остаются параллельными некоторому направлению.

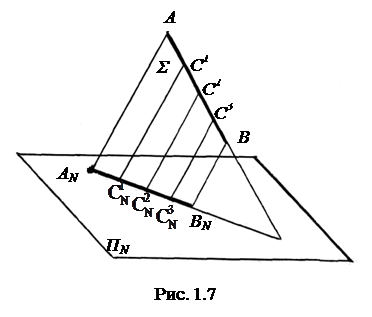Плоскость, образованная проецирующими лучами, называется проецирующей. Обозначим ее буквой Σ. При пересечении плоскостей Σ и П_N образуется прямая А_N B_N, которая является проекцией прямой АВ.

Инцидентность – взаимная принадлежность. Если точка лежит на прямой, то проекции точки лежат на проекциях прямой. Доказательство: пусть на прямой АВ (рис. 1.7) даны точки С¹, С² и С³. Проецирующие лучи, проходящие через эти точки, лежат в проецирующей плоскости Σ и пересекаются с проекцией прямой А_N B_N в точках , и , так как А_N B_N также лежит в плоскости Σ.

Эти три свойства относятся также и к центральной системе проецирования.

Деление отрезка в данном отношении. Если точка делит отрезок в некотором отношении, то проекция точки делит проекцию отрезка в том же отношении. Доказательство: пусть точка С¹ (рис. 1.7) делит отрезок АВ в отношении . Из рисунка видно, что прямая АВ и ее проекция А_N B_N лежат в одной проецирующей плоскости Σ и пересекаются.

Проецирующие лучи АА_N, С¹С 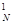и ВВ_N параллельны. Известно, что параллельные прямые отсекают на пересекающихся прямых пропорциональные части, следовательно .

Проекции параллельных прямых. Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 1.8). Доказательство: прямые АВ и CD проецируются с помощью проецирующих плоскостей Σ и Т, но Σ ║ Т, т. к. АВ ║ CD по условию и АА_N ║ СС_N - по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскости Σ и Т пересекаются плоскостью проекций П_N и образуются параллельные прямые (А_NВ_N ║ C_ND_N).

Проекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура - прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: дано Σ ║ П_N и АВ Σ (рис. 1.9). Требуется доказать, что АВ ║ А_NВ_N и АВ = А_NВ_N. Так как Σ ║ П_N , то отрезки АА_N и ВВ_N равны и параллельны. Следовательно, четырехугольник АВВ_NА_N является параллелограммом и АВ ║ А_NВ_N, АВ = А_NВ_N.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

Частный случай проецирования прямого линейного угла. Если плоскость угла не параллельна плоскости проекций, то в общем случае угол проецируется с искажением.

В частном случае для ортогонального проецирования имеет место следующее: если одна сторона прямого линейного угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол проецируется в натуральную величину ( рис. 1.10 ). При этом плоскость угла не параллельна плоскости проекций. Доказательство: дано АВ ВС; ВС ║ П_N; АВ ╫ П_N. Требуется доказать, что В_NС_N А_NВ_N.

Пусть АВ проецируется с помощью плоскости Σ, а ВС - с помощью плоскости Т, тогда:

1) ВС Σ, так как ВС АВ по условию и ВС ВВ_N по построению;

2) В_NС_N Σ, так как В_NС_N ║ ВС и ВС Σ;

3) В_NС_N А_NВ_N, так как если прямая перпендикулярна к плоскости, то она перпендикулярна любой прямой, лежащей в плоскости.

1.2.5. Проецирующие геометрические фигуры. Это геометрические фигуры, образованные проецирующими лучами. Проецирующими геометрическими фигурами могут быть:

- прямые - проецируют точки;

- плоскости - проецируют прямые линии и плоские фигуры;

- цилиндрические поверхности в параллельной системе проецирования и конические поверхности в центральной системе проецирования - проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следом данной проецирующей геометрической фигуры или ее главной проекцией.

На рис. 1.11 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскость Σ и проецирующая цилиндрическая поверхность Ф.

Прямая а, плоскость Σ и образующие цилиндрической поверхности Ф перпендикулярны плоскости проекций П_N . Их главные проекции а_N , Σ_N и Ф_N включают в себя проекции всех точек данной проецирующей геометрической фигуры.

1.2.6. Дополнения однокартинного чертежа. Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок. Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 1.12 даны проекции различных геометрических фигур с числовыми отметками.

Около проекции точки А стоит цифра 20. Это означает, что точка А отстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВС отстоят от плоскости на расстояниях 15 и 30, вершины треугольника DEF - на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость П_N горизонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскости П_N.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Способ применения двух плоскостей проекций. Точка проецируется на две плоскости проекций П₁ и П₂ (рис. 1.13). При ортогональном проецировании принято располагать плоскости проекций перпендикулярно друг другу (П₁ П₂).

Проекция точки на каждой плоскости проекций обозначается той же буквой, что и сама точка, но с индексом данной плоскости проекций. Так, проекция точки А на плоскость П₁ обозначается А₁.

Линия пересечения плоскостей проекций обозначается буквой х, около которой ставятся индексы плоскостей, линией пересечения которых она является, т.е. х₁₂.

Вторая плоскость проекций П₂ является дополнением однокартинного чертежа на П₁. Если даны проекции точек А₁ и А₂ на П₁ и П₂, то всегда можно определить положение точки в пространстве на пересечении перпендикуляров, восстановленных к плоскостям проекций из этих точек.

Таким образом, проекции точки на две взаимноперпендикулярные плоскости проекций дают полное представление о положении точки в пространстве. Способ дополнения однокартинного чертежа с помощью второй плоскости проекций в настоящее время принят в технике как основной.