Пересечение линии с поверхностью

3.4.1. Пересечение линии с поверхностью, когда оба геометрических объекта проецирующие. На рис. 3.16 показано пересечение фронтально-проецирующей плоскости Σ и горизонтально-проецирующей прямой m.

Так как плоскость Σ и прямая m проецирующие, то проекции точки их пересечения (точка K) на чертеже уже определены, их надо только отметить (K₂ и K₁).

3.4.2. Пересечение линии с поверхностью, когда один из пересекающихся геометрических объектов проецирующий, а другой – непроецирующий. На рис. 3.17 показано определение точки пересечения плоскости Σ (a||b) и прямой m.Σ∩m=K.

Так как прямая m┴Π₂ (рис. 3.17, а), то K₂≡m₂ (рис. 3.17, б), а K₁ находим из условия принадлежности точки K плоскости Σ с помощью вспомогательной прямой CE Î Σ. Ход построения указан на чертеже.

На рис. 3.18 показано построение точек пересечения прямых d и m с конической поверхностью Φ. d∩Φ=K, m∩Φ=C и B.

Так как d┴Π₁, то K₁≡d₁, а K₂ находим с помощью образующей S .

Прямая m┴Π₂, поэтому фронтальные проекции C₂ и B₂ точек пересечения прямой m с конусом совпадают с m₂, а C₁ и B₁ находим с помощью параллели.

3.4.3. Пересечение линии с поверхностью, когда оба геометрических объекта непроецирующие. Для определения точек пересечения линии с поверхностью (рис. 3.19) необходимо:

1) заключить линию (m)во вспомогательную поверхность: Σ 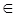m. Желательно, чтобы при пересечении Σ с заданной поверхностью Φ получались прямые или окружности;

2) определяем линию пересечения ℓ вспомогательной поверхности Σ и Φ. Σ∩Φ=ℓ;

3) определяем точки пересечения построенной линии ℓ с m, то есть ℓ∩m=K^ί;

4) определяем видимость заданной линии.

На рис. 3.20 показано построение точки пересечения прямой общего положения m с плоскостью Φ (a||b) (рис. 3.20, а) иm∩Φ=K (рис. 3.20, б).

Ход построения:

1) заключаем прямую m во фронтально-проецирующую плоскость Σ (Σ 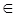m), то есть через m₂ проводим Σ₂;

2) строим линию пересечения плоскостей Σ и Φ. Это прямая CM (C₁M₁, C₂M₂). CM=Σ∩Φ;

3) определяем точку K пересечения m с CM. Сначала определяем точку K₁ (K₁= m₁∩C₁M₁), а затем с помощью линии проекционной связи - точку K₂ (K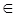₂ m₂);

4) видимость прямой m и плоскости Φ определяем с помощью конкурирующих точек: на Π₁ – с помощью N и F; на Π₂ – с помощью L и M.

 

На рис. 3.21 показано построение точек пересечения горизонтали h со сферой Φ.

Ход построения:

1) заключаем прямую h в горизонтальную плоскость Σ 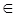h (Σ₂ ≡ h₂);

2) строим линию пересечения ℓ (окружность радиуса R) плоскости Σ со сферой. Σ ∩Φ=ℓ;

3) определяем точки пересечения линии ℓ с горизонталью h. ℓ∩h=K и M. Сначала отмечаем точки K₁ и M₁, а затем с помощью линий проекционной связи находим K₂ и M₂ на h₂;

4) определяем видимость линии m.

Построение точек пересечения прямой общего положения m со сферой Φ приведено на рис 3.22.

 

 

Для определения искомых точек пересечения выполним следующие построения:

1) заключаем прямую m в горизонтально-проецирующую плоскость Σ (Σ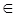₁ m₁).

При пересечении Σ со сферой получается окружность, которая на Π₂ спроецируется в виде эллипса. Чтобы избежать построения эллипса, с помощью метода замены плоскостей проекций преобразуем прямую m в положение линии уровня, тогда дальнейшее построение будет подобно примеру на рис. 3.21.

Для этого:

2) на прямой m задаём две точки A и B;

3) проводим дополнительную плоскость Π₄||m (х₁₄||m₁);

4) Проецируем на Π₄ прямую AB и сферу. В новой системе Π₁-Π₄ прямая m стала фронталью (m₁, m₄);

5 ) Σ∩Φ=ℓ (окружность радиуса R);

6 ) ℓ ∩ m=K и M, то есть ℓ₄ ∩ m₄=K₄ и M₄. K₁ и M₁, K₂ и M₂ находим по линиям проекционной связи;

7) Определяем видимость m на Π₁ и Π₂.

На рис. 3.23 показано построение точек пересечения прямой общего положения m с конусом.

В данном случае удобнее всего, чтобы вспомогательная плоскость Σ пересекала конус по двум образующим, то есть вспомогательная плоскость должна проходить через вершину конуса S. Эта плоскость уже задана на чертеже прямой m и точкой S, то есть Σ (S, m).

Для удобства построений переходим к заданию плоскости Σ пересекающимися прямыми. Для этого на прямой m задаём точку E (E₁, E₂) и соединяем её с вершиной S. Теперь плоскость Σ задана двумя пересекающимися прямыми: Σ (m∩SE).

Далее строим линию пересечения Σ с Π₁, это линия CM. Для этого находим горизонтальные следы прямых m и SE, это C₁ и M₁.

Горизонтальный след Σ (CM) и основание конуса лежат в одной плоскости, поэтому линия CM пересекает основание конуса в точках A и B, которые соединяем с вершиной S и получаем образующие AS и SB, по которым Σ пересекает конус.

Затем строим точки пересечения AS и SB с прямой m. AS∩m=K, BS∩m=F.

Таким образом точки K и F - искомые точки. Далее определяем видимость прямой m.