Среднеквадратичный критерий

 

Предполагает минимизацию суммы квадратов ошибки в узловых точках:

где y_i -значение исходной функции в точке х_i (табличное);

F(х_i) -значение аппроксимирующей функции.

Среднеквадратичный критерий позволяет получить сглаживание кривой, то есть позволяет отфильтровать зашумленные данные, не требуя никакой дополнительной информации о шумовых характеристиках помех.

 

МИНИМАКСНЫЙ КРИТЕРИЙ ИЛИ КРИТЕРИЙ ЧЕБЫШЕВА

 

Минимаксный критерий Чебышева определяется как:

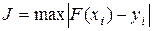
Если применение среднеквадратичного критерия уменьшает среднеквадратичную ошибку, при этом допуская отдельные большие ошибки, то чебышевское приближение - минимаксное - уменьшает экстремальную наибольшую ошибку. По этому этот критерий используется, когда необходимо при аппроксимации избежать больших ошибок.

Минимаксный критерий также не использует дополнительную информацию о шумовых характеристиках помех.

 

ВЕРОЯТНОСТНО-ЗОНАЛЬНЫЙ КРИТЕРИЙ

 

К данным критериям относится целая группа критериев. Данные критерии используют (требуют) дополнительную информацию о шумовых характеристиках объекта:

- обобщенный метод наименьших квадратов - ковариационные матрицы шума;

- максимальное правдоподобие - распределение вероятностей и т.д.

 

ТОЧНОСТЬ

 

Выбор точности приближения осуществляется исходя из условий задачи и выбранного критерия.

На практике наибольшее распространение получил метод наименьших квадратов, использующий среднеквадратический критерий.

 

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

ПОСТАНОВКА ЗАДАЧИ

 

Пусть задана таблица измерений:

 

xi	x1	x2	…	xn
F(x)	y1	y2	…	yn

 

Тогда задача формулируется следующим образом: для функции F(x_i), заданной таблицей, найти функции F определенного вида так, чтобы сумма квадратов:

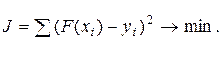
В качестве приближающих функций в зависимости от характера точечного графика функции f рассмотрим следующие функции:

- степенная

- показательная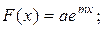

- дробно-линейная

- логарифмическая

- гиперболическая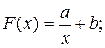

- дробно-рациональная

- линейная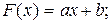

- квадратный трехчлен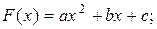

 

a, b, m, c – неизвестные параметры. Когда осуществлен выбор приближающей функции, то задача приближения сводится к определению значения этих параметров.

Рассмотрим задачу в общем виде.

Приближающая функция имеет общий вид:

Сумма квадратов:

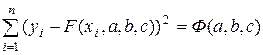
Чтобы найти минимум функции 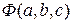, используем необходимое условие экстремума:

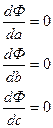
т. е.

 

Решив эту систему трех уравнений с тремя неизвестными а, в, с мы и получили конкретный вид функции F(x, a, b, c).

Естественно, что F(x_i) отличается от y_i, но отношения

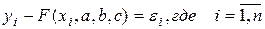
будут минимальны в среднеквадратичном случае.

Рассмотрим метод наименьших квадратов для различных функций.

ЛИНЕЙНАЯ ФУНКЦИЯ.

 

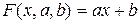
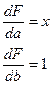
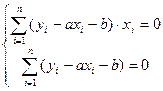
Разделив каждое уравнение на n, получается:

 

Введем обозначения:

 

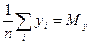
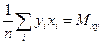
Таким образом, получается система линейных уравнений с неизвестными: a и b:

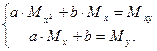
Разрешив данную систему уравнений относительно неизвестных параметров а и b, определим искомую функцию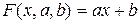

Результаты вычислений лучше всего оформить в виде таблицы

 

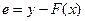
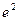
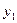
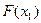
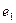
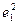
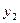
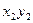
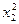
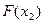
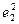
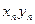
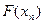
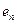
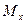
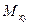
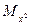
						E

 

Значение E определяет близость аппроксимирующей функции к исходной. E определяется по следующей формуле:

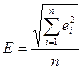
Естественно, чем меньше E, тем аппроксимирующая функция ближе к исходной функции.

КВАДРАТНЫЙ ТРЕХЧЛЕН.

 

 

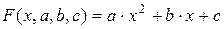
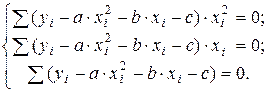
После преобразования получается система линейных уравнений с неизвестными: a, b, c.

Разрешив данную систему уравнений относительно неизвестных параметров а, b и с, определим искомую функцию .

Результаты вычислений лучше всего оформить в виде таблицы

 

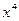
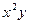
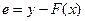
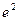
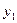
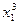
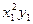
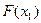
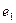
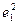
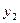
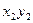
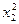
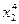
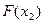
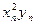
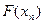
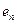
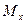
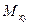
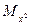
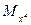
									E

 

СТЕПЕННАЯ ФУНКЦИЯ

Степенная функция имеет вид:

Если прологарифмировать данное уравнение, то можно получить следующее:

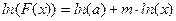
Введя новые переменные:

,

получим следующее линейное уравнение:

.

Определив параметры А и В (см. линейную функцию), можно определить параметры степенной функции:

Результаты вычислений лучше всего оформить в виде таблицы

 

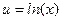
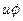
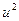
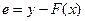
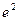
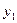
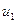
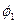
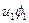
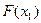
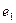
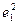
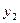
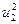
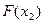
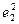
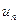
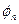
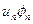
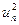
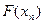
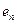
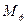
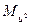
								E

Следует заметить, что данный алгоритм справедлив только для положительных значений x и y.

ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ.

 

Показательная функция имеет вид:

Если прологарифмировать данное уравнение, то можно получить следующее:

Введя новые переменные:

,

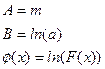получаем следующее линейное уравнение:

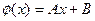
Определив параметры А и В (см. линейную функцию), можно определить параметры степенной функции:

Результаты вычислений лучше всего оформить в виде таблицы

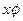
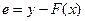
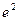
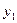
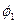
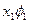
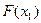
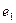
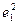
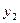
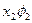
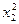
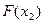
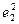
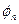
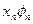
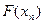
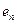
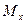
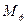
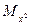
							E

Следует заметить, что данный алгоритм справедлив только для положительных значений y.

ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ.

 

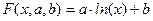
Введя новую переменную:

,

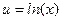получаем следующее линейное уравнение:

 

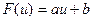
Результаты вычислений лучше всего оформить в виде таблицы

 

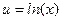
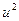
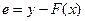
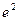
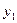
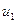
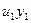
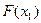
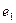
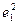
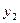
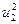
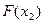
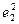
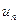
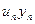
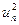
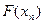
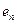
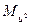
							E

Следует заметить, что данный алгоритм справедлив только для положительных значений u.

 

 

ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ.

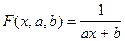
Преобразуем следующим образом:

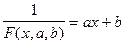
Введя новую переменную:

,

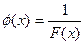получаем следующее линейное уравнение:

 

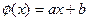
Результаты вычислений лучше всего оформить в виде таблицы

 

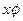
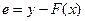
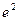
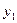
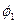
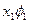
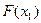
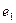
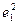
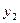
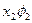
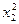
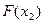
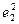
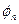
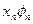
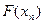
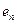
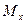
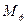
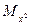
							E

Следует заметить, что данный алгоритм справедлив только для y, отличных от нуля.

 

ГИПЕРБОЛА.

 

 

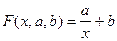
Введя новую переменную:

,

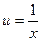получаем следующее линейное уравнение:

 

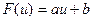
Результаты вычислений лучше всего оформить в виде таблицы

 

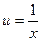
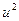
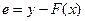
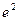
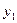
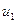
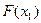
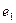
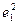
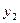
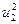
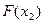
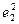
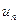
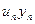
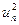
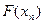
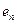
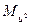
							E

 

ДРОБНО-РАЦИОНАЛЬНАЯ.

 

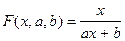
Преобразуем следующим образом:

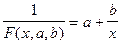
Введя новые переменные:

,

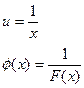получаем следующее линейное уравнение:

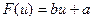
Результаты вычислений лучше всего оформить в виде таблицы

 

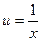
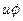
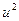
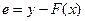
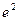
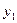
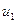
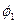
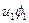
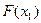
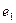
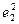
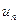
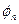
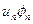
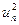
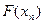
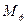
								E

Следует заметить, что данный алгоритм справедлив только для x и y, отличных от нуля.