Введение.
Понятие о численных методах.
История развития численных методов.
Современное развитие науки и техники тесно связано с использованием ЭВМ, ставшим рабочим инструментом учёного, инженера, конструктора. ЭВМ позволяет строить математические модели сложных устройств и процессов, при этом резко сократить время и стоимость инженерных разработок.
Широкое использование ЭВМ способствовало развитию вычислительной математики (прикладной математики). Как и любая наука, математика представляет собой сплав "классической" (теоретической) науки и прикладной науки, в роли последней выступает область вычислительных методов.
В основе вычислительной математики лежит решение задач математического моделирования численными методами. Решение задач этими методами даёт приближенное решение, но в ряде случаев это выгодно, так как не всегда представляется возможность разрешить математическую задачу аналитически, а методы решения настолько громоздки и трудоемки, то полученное решение становится приемлемым для проектного применения.
Разработанные на сегодняшний момент численные методы перекрыли практически всю классическую математику моделирования. Применение приближенных численных методов во многих случаях более предпочтительно даже тогда, когда известен точный метод решения, так как достаточная точность и небольшие затраты времени при использовании ЭВМ обеспечивают получение ценных результатов, не прибегая к громоздким выкладкам.
Главная задача вычислительной математики - фактическое нахождение решение с требуемой точностью, тогда как классическая математика решает в основном задачи существования и свойств решения.
Вычислительная математика начала свое развитие достаточно давно и в своем движении прошла три этапа:
I. Первый этап начался 3-4 тысячи лет назад. Он был связан с несложными задачами арифметики, алгебры и геометрии. Например, ведение конторских книг, вычисление площадей и объемов, расчетами простейших механизмов. Вычислительные средства- палочки, пальцы, камешки и вершина- счеты.
II. Второй период начался с Ньютона. В этот период решались задачи астрономии, геодезии и расчета механических конструкций, сводящиеся либо к обыкновенным дифференциальным уравнениям, либо к алгебраическим системам с большим числом неизвестных. Вычислительные средства- таблицы элементарных функций, арифмометры и логарифмические линейки.
III. Третий период начался примерно с 1940 года. Толчком к развитию прикладной математики послужили военные задачи, требующие высокой скорости и решения задач. Появились электронные вычислительные машины.
В основу изучения и практического использования численных методов положены следующие основополагающие тезисы:
1. Цель расчетов - это понимание, а не числа;
2. Прежде чем решать задачу, необходимо подумать над практическим применением ее решения;
3. ЭВМ многократно увеличивает некомпетентность вычислителя (инженера). До производства вычислений на ЭВМ необходимо представлять физическую сущность процессов, которые инженер моделирует с помощью программы на ЭВМ.
Интерполяция функций.
Первый этап работы любого вычисления - числа, приближения, погрешность.
Второй этап работы - функция, вычисления функции, её приближения. В краце о интерполяции. Интерполяция в простейшем случае заключается в следующем:
|
Постановка задачи.
На отрезке 
заданы n значений аргумента x и соответствующие им значения функции f(x0)=y0; f(x1)=y1; …; f(xn)=yn.
Требуется построить функцию F(x), которая бы принимала в точках x те же значения, что и f(x):
F (x0)=y0; F (x1)=y1… F (xn)=yn
Для чего?
Для того, чтобы:
1. Задача интерполяции. Суметь по полученной функции вычислить значения F(z), где z 
,
z 
xi при i=0,n
2. Задача экстраполяции. Суметь по полученной функции вычислить F(z), где z 
.
Все существующие интерполяционные формулы содержат в себе конечные разности различных порядков.
Введём понятие конечных разностей.
Конечные разности различных порядков.
Пусть: y =f(x) - заданная функция
- фиксированная величина приращения аргумента
Тогда 
- называется первой конечной разностью функции y, или конечной разностью первого порядка.
Вторая конечная разность, или конечная разность второго порядка.
Третья конечная разность, или конечная разность третьего порядка.
Т.о., в общем виде:
Конечная разность n -го порядка.
Пример: 
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной и диагональной таблиц разностей
| x | y | 
| 
| 
|
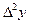
| x 0 | y 0 | 
| 
| 
|
| x 1 | y 1 | 
| 
| 
|
| ... | ... | ... | ... | ... |
Диагональная таблица разностей.
| x | y |
|
|
|
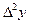
| X 0 | Y 0 | |||
|
| ||||
| X 1 | Y 1 |
| ||
|
| |||
| X 2 | Y 2 |
| ||
| ||||
| X 3 | Y 3 |
Пример: горизонтальная таблица функции y = f(x) = x2 при
, x 0 = 0 начальное значение, x 6=5 конечное значение
| x | y |
|
|
|
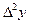
Диагональная таблица
| x | y |
|
|
|
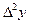
При составлении таблиц возможные ошибки вычисляются и диагональная таблица наглядно показывает нам, как отразится ошибка 
в значении y n.
| 
| 
| 
| 
| 
|
| 
| ||||
| |||||
| 
| 
| |||
| 
| ||||
| 
| 
| 
| ||
| 
| ||||
| 
| 
| 
| ||
| 
| ||||
| 
| 
| 
| ||
| 
| ||||
| 
| 
| 
| ||
| 
| ||||
| 
| 
| 
| ||
| 
| ||||
| 
| 
| |||
| |||||
| 
|
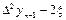
Следует заметить, что максимальная ошибка 
– в той же горизонтальной строке, где и табличная величина yn.
Пример: исправить ошибку в таблице (неверные цифры взяты в скобки).
| 
|
|
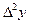
| Ошибка |
| 13,260 | ||||
| 14,144 | ||||
| 15,912 | ||||
| 15,028 | (-4)0 | |||
| 88(0)4 | ||||
| 16,79(2)6 | (8)0 | 
| ||
| 88(8)4 | ||||
| 17,680 | (-4)0 | 
| ||
| 18,564 |
| |||
| 19,448 | ||||
| 20,332 |
Как видно из таблицы, ход вторых разностей нарушается при x= 19. Ошибка распространяется на 3 строки. Находим среднее арифметическое значение второй разности для средней из 3 точек:
= 
, 
= 
Внося исправление в табличное значение y для x= 19, получим верное значение функции:
n=(y n+ )- =16.792-(-0.004)=16.796.
