Пусть на отрезке [ a;b ] даны n+ 1 различных значений аргумента x: x 0, x 1,…, xn и известны соответствующие их значению функции y=f(x): f(x 0 )=y 0, f(x 1 )=y 1, f(xn)=yn. Требуется построить полином 
степени не выше 
, имеющий в заданных узлах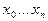 
те же значения, что и функция 
, т.е. Ln(xi)=yi при i=1,n
;
,
где Li(n) - коэффициенты Лагранжа.
Следует отметить, если узлы равностоящие, то интерполяционный полином Лагранжа совпадает с интерполяционной формулой Ньютона.
Примечательно то, что формула Лагранжа зависит лишь от yi, а не от разностей.
Частные случаи.
n= 1
При n= 1 имеем 2 точки: (x 0; y 0 ) и (x 1; y 1 ).
прямая, проходящая через эти точки-
n= 2 (x 0; y 0 ), (x 1; y 1 ), (x 2; y 2 )
Пример:
| 
| 
|
L 3 (x)=x 3 +x 2 -x+ 2
Для вычисления лагранжевых подмножеств удобно составлять следующую таблицу разности:
| x-x0 | x0-x1 | x0-x2 | ….. | x0-xn |
| x1-x0 | x-x1 | x1-x2 | ….. | x1-xn |
| x2-x0 | x2-x1 | x-x2 | ….. | x2-x1 |
| ….. | ….. | ….. | ….. | ….. |
| xn-x0 | xn-x1 | xn-x2 | ….. | x-xn |
Обозначим произведение элементов i -ой строки через Di, а произведение главной диагонали Пn+ 1 (x). Отсюда следует, что:
Пn+1(x)=(x-x 0 )(x-x 1 )…(x-xn)
при i=1,n
Для упрощения вычислений можно использовать инвариантность (при равноотстоящих точках лагранжевых коэффициентов),если
x= at+b
xj= atj+b при j=0,n
то Li(n)(x)= Li(n)(t)
Схема Эйткена
Чаще всего требуется найти не общее выражение Ln(x), а значение его при конкретных x, тогда будет удобно пользоваться интерполяционной схемой Эйткена:
Последовательно вычисляются многочлены:
и т.д.
Вычисления по схеме Эйткена удобно расположить в таблице:
| Xi | Yi | Xi-X | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i |
| X0 | Y0 | X0-X | L01 | L012 | L0123 |
| X1 | Y1 | X1-X | L12 | L123 | L1234 |
| X2 | Y2 | X2-X | L23 | L234 | |
| X3 | Y3 | X3-X | L34 | ||
| X4 | Y4 | X4-X |
Вычисления по схеме Эйткена обычно ведутся до тех пор, пока последовательные значения L 01… n(x) и L 01… n(n+ 1 ) не совпадут по заданной точности.
Т.е. процедура является итерационной, легко реализуется и этим обеспечивает возможность автоматического контроля точности вычислений.
Пример: x= 27, 
=0,1
| i | xi | yi | xi-x | Li-1,i | Li-2,i-1,i | Li-3,i-2,i-1,i | Li-4,i-3,i-2,i-1,i |
| 68,7 | -13 | 48,33 | 49,38 | 49,31 | |||
| 64,0 | -10 | 49,71 | 49,26 | ||||
| 44,0 | 48,90 | 48,21 | |||||
| 39,1 | 50,46 | ||||||
| 32,0 |
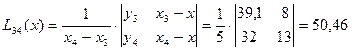
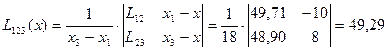
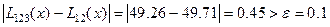
Формула Ньютона для неравностоящих узлов
Разделённые разности
Если в таблицах встречаются неравноотстоящие значения аргумента, т.е. таблицы с переменным шагом, то вводят понятие разделённых разностей.
Пусть функция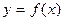 
задана таблично, где
- значения аргумента
- значения функции
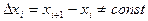
отношения 
- разделённая разность первого порядка
- разделённая разность второго порядка
- разделённая разность -го порядка
Разделённые разности удобнее всего рассматривать в таблице - таблице разностей
|
|
| Разделённые разности | ||||||
| 1-го | 2-го | 3-го | 4-го | |||||
| 
| |||||||
| ||||||||
| 
| 
| ||||||
| 
| |||||||
| 
| 
| 
| |||||
| 
| |||||||
| 
| 
| ||||||
| ||||||||
| 
| |||||||
Интерполяционная формула Ньютона для неравностоящих значений аргумента
Дано 
- значения аргумента
- значения функции
Апроксимировать таблично заданную функцию полиномом порядка не выше
Пример:
| 
| 1-го | 2-го | 3-го |
| 1,450 | ||||
| 1,127 | ||||
| 1,5 | 3,140 | -0,098 | ||
| 0,795 | - 0,012 | |||
| 3,4 | 4,650 | -0,18 | ||
| -0,159 | ||||
| 6,8 | 4,110 |
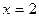
Погрешность формулы Ньютона для неравностоящих узлов
где - промежуточное значение между точкам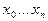и и
Интерполяция сплайками
Даны: 
, разбитый на разные отрезки с узлами 
и соответствующие им значения функции 
Сплайком называется функция, которая вместе с несколькими производными непрерывна на заданном отрезке , и на каждом частичном отрезке 
в отдельности является некоторым алгебраическим многочленом, причём степени многочлена различны.
Степень сплайка - максимальная степень многочлена.
Дефект сплайка - разность между степенью сплайка и порядком наивысшей производной на отрезке .
На практике широкое применение получили кубические сплайки.
Таким образом для интерполяции сплайками, необходимо знать не только значения функции в точках 
и 
; а ещё и их производные
- наклон сплайка
Как задаётся наклон сплайка?
1. Упрощённый способ
2. Если известны значения 
=> 
3. Глобальный
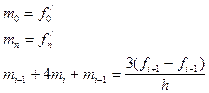
Сплайки являются наиболее удобным средством апроксимации функций на небольших промежутках, то есть 
.
При апрксимации функций интерполяционными многочленами можно потребовать очень высокой степени полиномы, тогда как разбиения на участки, содержащих несколько участков, правда при этом в савке двух многочленов первая производная терпит разрыв.
Многочлены Чебышева
Особенность интерполяции функции многочленами Чебышева заключается в том, что приведённые многочлены минимизируют максимальную погрешность 
