Быстрота сходимости процесса Ньютона

Если выполнимы все четыре условия теоремы 1, то для последовательных приближений , справедливо неравенство:

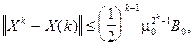
где - искомое решение, а

При сходимость метода - сверхбыстрая.

 

Единственность решения

Если выполнимы все четыре условия, в области

то содержится единственное решение системы

 

Выбор начального условия

Если выполнимы все четыре условия и , то процесс сходится к единственному решению в основной области при любом выборе начального условия из области

 

Модифицированный метод Ньютона

При использовании метода Ньютона наиболее трудоёмким является процесс вычисления обратной матрицы Якоби.

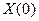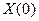Если матрица невырождённая для некоторого приближения , и достаточно близко к (искомому решению), то можно использовать модифицированный метод Ньютона.

 

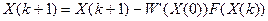
Метод итераций

Дана система нелинейных уравнений:

или

(1)

Допустим, что систему 1 можно привести к виду:

(2)

Введём обозначения:

, ,

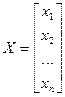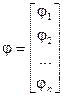Можно систему уравнений 2 переписать в виде:

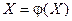
Приведённое матричное уравнение и есть формула метода итераций

 

Необходимое и достаточное условие сходимости процесса итерации

Пусть функции и 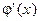непрерывны в области , причём в области выполнимо неравенство:

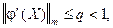
где 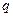- некоторая константа.

Если последовательные приближения

,

не выходят из области , то этот процесс сходится к единственному решению системы.

 

Следствие:

оценка пиближённо

На практике лучше всего рассматривать матрицу с элементами

Для сходимости должно выполнятся условие

1)

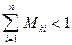
2)

3)

 

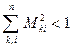
Метод скорейшего спуска (градиентный метод)

Дана система линейных уравнений:

(1)

В матричном виде

Считаем, что действительны и непрерывно дифференцируемы в их общей области определения.

Рассмотрим функцию

(2)

Очевидно, что если мы найдём решение системы уравнений 1 , то это решение является и решением системы уравнений 2 и наоборот.

Предполагаем, что система 1 имеет лишь одно изолированное решение, представляющего собой точку строго минимум функции . Таким образом задача сводится к нахождению минимум функции в -мерном пространстве.

Берём точку 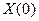- нулевое приближение. Через точку 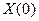проходит поверхность уровня и . Если 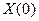близка , то поверхность = будет похожа на элипсоид.

Из точки 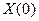движемся по нормали к поверхности до тех пор, пока эта нормаль не коснётся другой поверхности:

И так далее.

Так как , то двигаясь таким образом, мы быстро приближаемся к точке с минимальным значением , которая соответствует некоему корню .

 

Градиент функции U

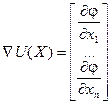
- набла или grad - есть вектор приложенный к точке , имеющий направление нормали. Из векторных произведений

, (3)

Как определить ? Для этого рассматривают скалярную функцию :

Уравнение 3 можно преобразовать так, чтобы не было явного выражения градиента. Введем обозначения , тогда итерационная формула градиентного метода будет иметь вид:

,

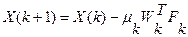где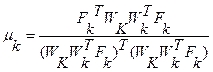

Вычисления производятся до тех пор, пока не станет справедливым следующее неравенство:

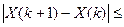e,

где e - заданная точность вычисления.

 

Пример. Дана система нелинейных уравнений:

Найти решение системы градиентным методом с точностью e=0,01

Определим начальное приближение как:

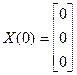
Вектор-функция имеет вид:

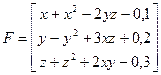
Якобиан, или матрица частных производных имеет вид:

1 итерация

 

 

 

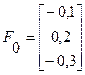
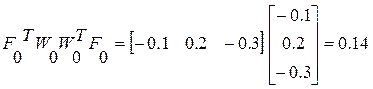
2 итерация

 

 

 

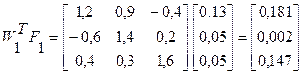
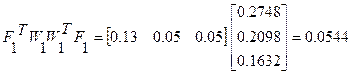
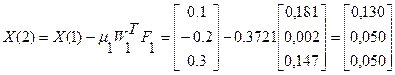
Решение системы нелинейных уравнений представлено в таблице:

 

K	x	½Dx½	y	½Dy½	z	½Dz½
	0.000	0,100	0.000	0,200	0.000	0,300
	0.100	0,030	-0.200	0,250	0.300	0,250
	0,130	0,095	0,050	0,251	0,050	0,209
	0,035	0,018	-0,201	0,016	0,259	0,013
	0,017	0,003	-0,185	0,007	0,246	0,001
	0,014		-0,178		0,245

 

Таким образом, решение системы уравнений имеет вид: