ПОСТАНОВКА ЗАДАЧИ
Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости:
| x | x1 | x2 | … | xn |
| F(x) | y1 | y2 | … | yn |
Необходимо найти формулу, выражающую эту зависимость аналитически.
Необходимо отметить, что такая постановка задачи соответствует постановке задачи интерполяции. Однако в теории обработки экспериментальных данных методы отличаются от методов интерполяции, ранее рассмотренных.
Интерполяционные формулы позволяют построить полиномы, значения которых в узловых точках x1 совпадают со значениями y1. Однако такое совпадение в общем случае не означает совпадение характеров поведения исходной и интерполирующей функции. Требования неукоснительного совпадения значений исходной и интерполирующей функции может оказаться тем более неоправданным, если значения y1 получены в результате измерений и являются сомнительными. Это во-первых.
Во-вторых, задача интерполяции известными методами, как правило, решается для небольшого отрезка, и найденная, интерполяционная функция может оказаться непригодной для другого отрезка или даже для большего отрезка.
Исходя из вышесказанного, следует уточнить задачу методов обработки экспериментальных данных. По заданным табличным данным необходимо найти функцию заданного вида: y = F (x), которая в точках xi принимает значения как можно более близкие к табличным значениям yi.
Практически вид приближающей функции F можно определить следующим образом. Строится точечный график функции, заданной таблично, а затем проводиться плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой устанавливается вид приближающей функции (обычно из числа простых по виду аналитических функций).
Как правило, перед тем, как решить такую задачу необходимо ответить на четыре вопроса:
1) Какие узлы будут использоваться?
2) Какую аналитическая функция будет использоваться?
3) Какой критерий согласия будет использоваться?
4) Какую точность необходимо достичь?
УЗЛОВЫЕ ТОЧКИ
В принципе это вопрос статистики, а именно той области, которая называется "планированием эксперимента".
На практике узловые точки заданы внешними обстоятельствами или используются равноотстоящие точки.
Если же существует возможность выбора точек, то выбор осуществляется по формуле Чебышева, как и в методах интерполяции.
КЛАСС ФУНКЦИЙ
Выбор вида функции осуществляется исходя из общей задачи, в рамках которой решается задача обработки экспериментальных данных. В качестве функции приближения могут быть использованы следующие элементарные функции:
- степенная 
- показательная 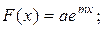
- дробно-линейная 
- логарифмическая 
- гиперболическая 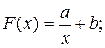
- дробно-рациональная 
- линейная 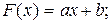
- квадратный трехчлен 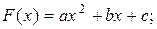
КРИТЕРИЙ СОГЛАСИЯ
Это самый важный вопрос. Решение этого вопроса дает ответ решения задачи наилучшего приближения. Что означает математически наилучшее приближение? Это означает выбрать критерий согласия, который является функцией невязки узловых точек и значениями аппроксимирующей функции:
 .
.
Выбор наилучшей функции осуществляется по минимуму этого критерия.
Существуют три наиболее широко распространенных критерия согласия:
- среднеквадратичный;
- минимаксный или Чебышева;
- вероятностно-зональный.






