Решение. Подберем ряд для сравнения. С учетом неравенств 
, 
, выполненных при всех 
, имеем
.
Для ряда 
воспользуемся интегральным признаком Коши. Положим 
. Тогда
.
Следовательно, и ряд 
, и ряд 
сходятся.
Функциональным рядом называется выражение вида
Для каждого фиксированного значения параметра 
сходимость ряда определяется как предел частичных сумм соответствующего числового ряда. Область сходимости – множество значений , при которых ряд сходится. Для степенного ряда
областью сходимости является интервал 
, где 
. Здесь 
обозначает верхний предел последовательности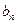 
, то есть наибольший из пределов всех сходящихся подпоследовательностей 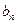. Внутри данного интервала ряд сходится абсолютно (то есть сходится ряд, составленный из модулей членов). Сходимость степенного ряда в граничных точках 
исследуется отдельно.
Рядом Тейлора функции 
в точке 
называется степенной ряд
где
.
Если значение равно сумме ее ряда Тейлора 
, то функция называется аналитической в точке . Ряд Тейлора определен однозначно в том смысле что, если 
для какого-либо степенного ряда, то тогда 
. Степенные ряды внутри области сходимости можно почленно дифференцировать и интегрировать: если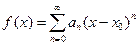 
, то тогда
,
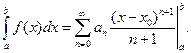
Задача 4.4. Выписать ряд Тейлора функции 
с центром в точке 
. Найти область сходимости ряда.
Решение. Воспользуемся формулой суммы бесконечной геометрической прогрессии:
при 
.
Для этого сначала поделим с остатком числитель дроби на знаменатель:
.
Далее,
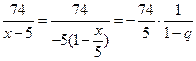где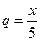 
.
Следовательно,
.
Окончательно,
Чтобы найти область сходимости ряда, воспользуемся признаком Даламбера. Зафиксируем и рассмотрим ряд из модулей:
Тогда общий член ряда записывается формулой 
, 
, и, следовательно,
Согласно признаку Даламбера при 
ряд сходится, а при 
ряд расходится. Интервал сходимости ряда 
. Исследуем поведение ряда в граничных точках 
. При 
получаем:
.
Поскольку 
, то необходимое условие сходимости ряда оказывается невыполненным, и ряд расходится. При 
ряд расходится по той же причине.
Задача 4.5. Вычислить приближенно с точностью до e =0.001 значение интеграла 
, используя разложение подынтегральной функции в ряд Тейлора.
Решение. Воспользуемся формулой
Подставляя 
вместо 
, получим:
.
Интегрируя почленно, получим
Чтобы понять, сколько членов ряда нужно взять, чтобы найти сумму ряда с точностью до 0.001, воспользуемся оценкой остатка лейбницевского ряда: сумма отброшенных слагаемых по модулю не превосходит первого отброшенного числа. Таким образом, остается решить, для какого натурального числа впервые будет выполнено неравенство
.
Последовательно подставляя в данное неравенство значения 
, убеждаемся, что впервые неравенство оказывается выполненным при 
:
.
В частности, все слагаемые ряда, начиная с 
, можно отбросить.
Ответ: 
.
Рядом Фурье на интервале 
называется функциональный ряд вида
Если функция непрерывна (или имеет конечное число разрывов первого рода) на интервале , и ее производная существует всюду, кроме конечного числа точек, и при этом ограничена по модулю 
, то значение в точках непрерывности равно сумме ряда Фурье
,
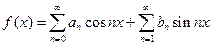коэффициенты 
и 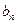которого определяются по формулам
, 
, 
, 
,.
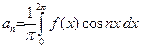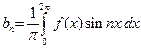Задача 4.6. Представить функцию 
рядом Фурье в интервале (0,2p).
Решение. Имеем:
.
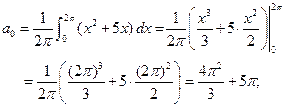
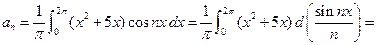
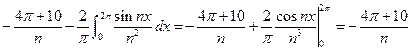Окончательно, получаем:
.
Литература.
1. Щипачев В.С. Высшая математика. Учебник для вузов. - М., Высшая школа, 2001.
2. Кремер Н.Ш. Высшая математика для экономистов. Учебник. 2 издание. Юнити - Дана, 2002.
3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., Наука, 1984.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М., Наука, 1988.
5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. ТФКП. - М., Наука, 1985.
6. Клетеник Д.В. Сборник задач по аналитической геометрии. - М., Наука, 1984.
7. Борисова О.Н. Математика: Учебная программа и методические материалы. - Королев: КИУЭС, 2003, 26 с.
СОДЕРЖАНИЕ
| Раздел | Стр. | |
| Линейная алгебра | ||
| Векторная алгебра и аналитическая геометрия | ||
| Пределы | ||
| Производная | ||
| Функции нескольких переменных | ||
| Интегралы | ||
| Дифференциальные уравнения | ||
| Ряды | ||
| Литература | ||
| Содержание |
