Дифференциальным уравнением первого порядка называется любое уравнение вида
.
Решением дифференциального уравнения называется функция 
, подстановка которой в 
обращает уравнение в тождество:
.
Если уравнение можно разрешить относительно производной 
, то говорят, что уравнение записано в нормальной форме:
.
Задача Коши для уравнения заключается в нахождении решения , удовлетворяющего условию 
. Теорема о существовании и единственности решения задачи Коши утверждает, что, если функция 
и её частная производная 
непрерывны по совокупности аргументов, то найдется такой интервал 
, на котором имеется, и притом единственное, решение уравнения , для которого .
Общее решение дифференциального уравнения 1-го порядка есть соотношение вида 
такое, что
1) для любого решения уравнения найдется константа 
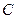, для которой 
;
2) для любой константы 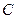неявное уравнение определяет некоторое решение дифференциального уравнения .
Имеется несколько стандартных уравнений первого порядка, в которых нахождение общего решения сводится к взятию подходящих интегралов.
Уравнения с разделяющимися переменными. Эти уравнения имеют вид
.
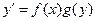Решение уравнения сводится к преобразованию
Û 
Задача 4.1.а) Найти общее решение дифференциального уравнения 
Решение. Запишем как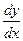 
и перегруппируем правую и левую части уравнения, так чтобы слева от знака равенства остались члены, зависящие только от 
, а справа –только от 
.
Вычисляя интеграл от левой части, получим:
.
Для правой части получаем
.
Окончательно,
.
Однородные уравнения. Уравнения имеют вид
.
Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью замены
, 
,
откуда следует, что
Û 
.
Задача 4.1.б) Найти общее решение дифференциального уравнения 
Решение. Правая часть уравнения является функцией от 
, поскольку 
. Будем искать решение в виде 
. Тогда 
, и исходное уравнение можно записать в следующем виде
Û 
.
Разделяем переменные
Û 
,
откуда
Для первого слагаемого получаем:
.
Для второго,
.
Следовательно,
.
С учетом табличного интеграла
,
получаем
.
Остается вернуться к переменной .
Ответ: 
.
Линейные уравнения. Линейные уравнения имеют вид
,
где 
и 
произвольные функции. Для решения линейных уравнений будем использовать метод Бернулли. Он заключается в том, что решение ищется в виде произведения двух функций 
, одну из которых мы выберем специальным образом. С учетом соотношения
,
получим
.
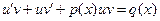В качестве 
возьмем произвольное решение уравнения с разделяющимися переменными
.
Тогда 
, и функция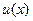 
есть решение уравнения
.
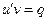Задача 4.1.в Найти общее решение дифференциального уравнения 
Решение. Положим 
, тогда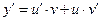 
и мы получаем
.
Выберем в качестве функции произвольное частное решение уравнения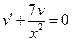 
. Тогда уравнение эквивалентно системе двух уравнений
Первое уравнение представляет собой уравнение с разделяющимися переменными:
Û 
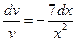Û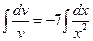 
,
откуда
.
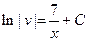Поскольку нас интересует частное решение этого уравнения, положим 
. Тогда
Û 
.
Второе уравнение системы теперь можно записать в виде
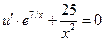Û 
,
откуда
Ответ: 
Уравнения Бернулли. 
Уравнения Бернулли либо сводятся к линейным с помощью замены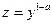 
, либо интегрируются с помощью подстановки Бернулли .
Задача 4.1.г Найти общее решение дифференциального уравнения 
Решение. Воспользуемся подстановкой Бернулли
, ,
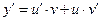откуда
Приравнивая нулю сумму второго и третьего слагаемых, получим систему
Находим частное решение первого уравнения
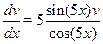Û 
,
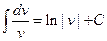Следовательно,
.
Полагая , получим
.
Для второго уравнения системы теперь получаем
,
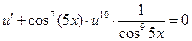откуда
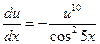Û 
.
Для интеграла слева получаем
.
Для интеграла справа получаем
.
Следовательно,
Û 
.
Вовзращаясь к , получим
