Определенный интеграл (Римана) позволяет распространить формулу площади прямоугольника на площадь более или менее произвольной плоской геометрической фигуры. В основе понятия определенного интеграла лежит так называемая интегральная сумма, определяемая следующим образом. Пусть задана функция  , определенная на отрезке
, определенная на отрезке  . Разобъем отрезок
. Разобъем отрезок  произвольным образом на
произвольным образом на 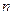 частей
частей 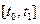 ,
,  ¼,
¼,  (
(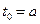 ,
,  ). В частности, можно разбить
). В частности, можно разбить  на
на 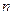 равных частей, тогда длина каждого отрезка разбиения будет равна
равных частей, тогда длина каждого отрезка разбиения будет равна  . В общем случае, пусть
. В общем случае, пусть
 .
.
Возьмем, опять же произвольным образом, внутри каждого из отрезков  по точке
по точке  . Интегральной суммой функции
. Интегральной суммой функции  на
на  по разбиению
по разбиению  называется число
называется число

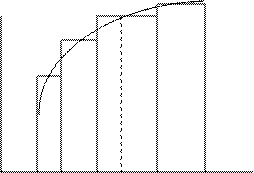






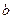
Если  , то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонами
, то интегральная сумма есть площадь фигуры, состоящей из прямоугольников со сторонами  и
и  ,
,  . Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения
. Интуитивно ясно, что, чем меньше максимальная длина отрезков разбиения  , тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями
, тем точнее эта фигура из прямоугольников приближает криволинейную трапецию с основаниями 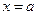 ,
,  и “боковыми сторонами”
и “боковыми сторонами”  ,
,  . Интеграл от функции
. Интеграл от функции  по отрезку
по отрезку  есть предел
есть предел  по всевозможным разбиениям
по всевозможным разбиениям  , когда
, когда  .
.
Предел понимается здесь в обычном смысле: число  называется определенным интегралом от
называется определенным интегралом от  по
по  (обозначается как
(обозначается как  ), если для произвольного
), если для произвольного  найдется такое
найдется такое 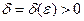 , что, как только разбиение
, что, как только разбиение  отрезка
отрезка  удовлетворяет условию
удовлетворяет условию  , интегральная сумма
, интегральная сумма  , отвечающая этому разбиению, будет отличаться от
, отвечающая этому разбиению, будет отличаться от  не больше, чем на
не больше, чем на  :
:  .
.
Геометрический смысл определенного интеграла.
Значение  (с точностью до знака) есть площадь криволинейной трапеции, заключенной между графиком функции
(с точностью до знака) есть площадь криволинейной трапеции, заключенной между графиком функции  , осью абсцисс и прямыми
, осью абсцисс и прямыми 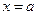 ,
,  . В частности, если на отрезке
. В частности, если на отрезке  заданы две функции
заданы две функции  и
и  , причем
, причем  , то площадь криволинейной трапеции, заключенной между графиками этих двух функций, равна
, то площадь криволинейной трапеции, заключенной между графиками этих двух функций, равна  .
.
Связь между определенным и неопределенным интегралом заключена в формуле Ньютона-Лейбница:
 ,
,
или, в другой записи,  , где
, где  - произвольная первообразная функции
- произвольная первообразная функции  .
.
Справедливы следующие две формулы – замена переменной интегрирования и интегрирование по частям.
Замена переменной.
Пусть  - произвольная непрерывно дифференцируемая функция, определенная на некотором отрезке
- произвольная непрерывно дифференцируемая функция, определенная на некотором отрезке  , причем
, причем  ,
,  , и
, и  при любом
при любом  . Тогда
. Тогда

Интегрирование по частям.
 .
.
Задача 3.6.а. Найти площадь фигуры, ограниченной линиями  ,
,  .
.
Решение. Заметим, что первое уравнение является уравнением параболы, ветви которой направлены вправо. Второе уравнение определяет прямую линию.
Найдем пересечения графиков функций и сделаем рисунок. Для этого решим систему
 Û
Û 
откуда  , что дает
, что дает  и
и  .
.
 3
3 
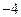
 0
0 
Из рисунка видно, что фигура состоит из двух частей. При  получаем сегмент параболы
получаем сегмент параболы  . При
. При 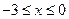 криволинейная трапеция заключена между прямой и параболой
криволинейная трапеция заключена между прямой и параболой  . Следовательно, площадь фигуры равна сумме двух следующих двух интегралов:
. Следовательно, площадь фигуры равна сумме двух следующих двух интегралов:
 Для первого интеграла получаем:
Для первого интеграла получаем:

Для второго интеграла получаем:

Таким образом,  . Ответ:
. Ответ:  .
.
Задача 3.6.б. Найти площадь фигуры, ограниченной линиями  ,
,  ,
, 
 .
.
Решение. На отрезке  выполняется неравенство
выполняется неравенство  . Поэтому найдем площадь, используя формулу
. Поэтому найдем площадь, используя формулу  .
.






 =
=  .
.






