1°)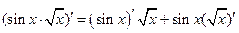 
2°) 
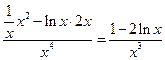
3°) 
4°)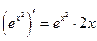 
5°)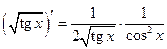 
6°)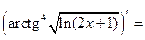 
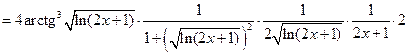
В задачах 2.2.а-2.2.з для функции 
требуется найти производную 
.
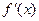Задача 2.2.а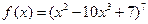 
.
.
Задача 2.2.б 
.
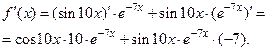
Задача 2.2.в 
.
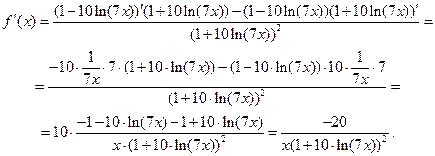Задача 2.2.г 
.
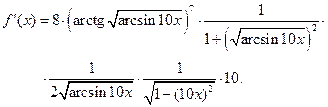
Задача 2.2.д 
.
Решение. При дифференцировании этой функции удобно воспользоваться приемом, который называется логарифмическим дифференцированием. Прежде чем вычислять производную, найдем логарифм функции :
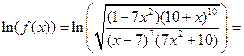
Теперь продифференцируем правую и левую часть полученной формулы, а затем приравняем соответствующие производные. Имеем:
;
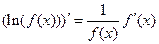Отсюда,
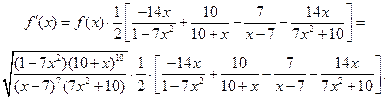
Задача 2.2.е 
.
Решение. Здесь также удобно воспользоваться приемом логарифмического дифференцирования.
;
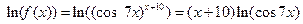откуда следует, что
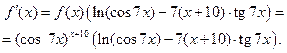
Задача 2.2.ж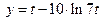 
, 
.
Решение. Функция 
задана в параметрической форме, поэтому следует воспользоваться формулой для параметрической производной:
Получаем:
,
,
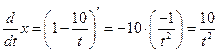откуда
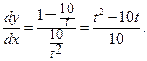
Задача 2.2.з 
.
Решение. Функция задана неявным уравнением. Чтобы найти производную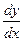 
, продифференцируем тождество 
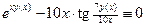. Получаем:
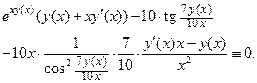
Перегруппируем слагаемые, выделяя члены, содержащие производную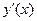 
:
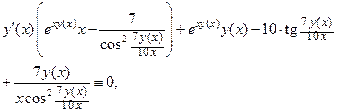
откуда следует, что
Непрерывность и типы разрыва функций.
Имеется три типа разрывов функций.
а) Устранимый разрыв, когда существует предел функции в точке 
, но он не равен значению функции в предельной точке
.
б) Разрыв первого рода, когда в точке существует предел слева и предел справа, однако они не равны между собой
.
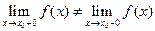в) Все остальные виды разрыва называются разрывами второго рода.
Задачи 2.3.а-2.3. б. Найти точки разрыва функций
, 
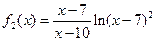
и определить тип разрыва. Сделать схематический чертеж.
Решение. Функция 
может иметь разрыв в точках 
, 
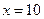. В точке в пределе 
имеет место соотношение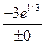 
, то есть функция 
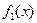становится неограниченной в окрестности . Поскольку 
при 
, и 
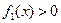при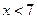 
, то функция 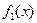стремится к 
при 
, и к 
при 
.
В точке 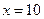ситуация сложнее. При 
в пределе получаем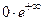 
, то есть мы имеем дело с неопределенностью. Чтобы найти предел 
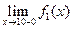, воспользуемся правилом Лопиталя:
.
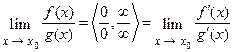Получаем: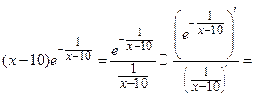 
Следовательно, 
В случае правостороннего предела ситуация проще:
Таким образом, в точке 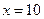также имеет место разрыв второго рода.
Схематическое поведение графика 
изображено на рисунке.
0 7 10 
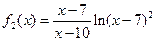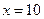Функция может иметь разрывы только в точках и . В окрестности точки 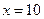функция 
имеет разрыв второго рода. При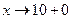 
получаем, что 
, а при получаем, что 
.
Найдем пределы при и при . Вновь используем правило Лопиталя. Пусть сначала .
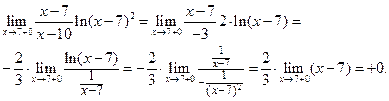
При 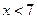вычисления аналогичны:
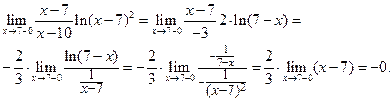
Следовательно, у функции в точке имеется устранимый разрыв. Эскиз графика изображен на рисунке.
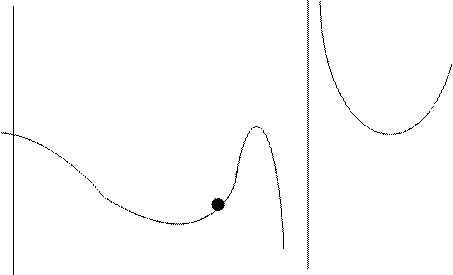
6 7 8 10
