Явление интерференции состоит в наложении световых волн с перераспределением светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности.
Необходимые условия интерференции:
- когерентность световых волн, т.е. равенство частот и постоянство разности фаз;
- поляризация световых волн в одной плоскости, т.е. чтобы колебания светового вектора  интерферирующих волн совершались вдоль одного и того же направления.
интерферирующих волн совершались вдоль одного и того же направления.
Волны, излучаемые любыми независимыми источниками света, всегда некогерентны и не являются поляризованными. Причина заключается в механизме испускания света атомами светящегося тела. Поэтому для осуществления интерференции необходимо волну, излучаемую реальным источником, разделить на две и заставить их пройти различные оптические пути, а затем наложить друг на друга.
Оптическим путем называется произведение показа- теля преломления среды  на геометрическую длину пути луча
на геометрическую длину пути луча  в данной среде:
в данной среде:
 (5.5)
(5.5)
Разность оптических длин, проходимых волнами путей, называется оптической разностью хода:
 . (5.6)
. (5.6)
Пусть разделение на две когерентные волны происходит в точке О, а наложение волн в точке Р (рис.5.1). Если  - фаза колебания в точке О, тогда первая волна возбудит в точке Р колебание
- фаза колебания в точке О, тогда первая волна возбудит в точке Р колебание
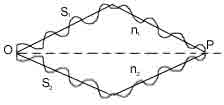
| Рис. 5.1 |
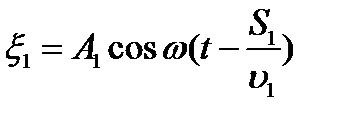 , (5.7)
, (5.7)
а вторая – колебание
 , (5.8) где
, (5.8) где 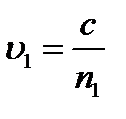 и
и  - фазовые скорости волн,
- фазовые скорости волн,  и
и  - амплитуды световых волн.
- амплитуды световых волн.
Амплитуда результирующего колебания
 , (5.9)
, (5.9)
где  ,
,  .
.
Разность фаз колебаний в точке Р равна

Учитывая, что  , а
, а  , получим
, получим
 . (5.10)
. (5.10)
Если разность фаз 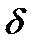 кратна
кратна  , то в точке Р колебания усиливают друг друга
, то в точке Р колебания усиливают друг друга
 ,
,
отсюда следует условие максимума интерференции
 , (5.11)
, (5.11)
где 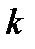 =0,1,2…
=0,1,2…
Если 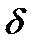 кратна нечетному числу
кратна нечетному числу  , то колебания ослабляют друг друга
, то колебания ослабляют друг друга
 ,
,
| Рис. 2.3 |
 , (5.12)
, (5.12)
где 
Способы получения когерентных световых волн
А) Метод зеркал Френеля

| Рис. 5.2 |
| Рис. 2.2 |
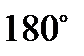 (рис.5.2). Парал- лельно линии пересечения зеркал на расстоянии
(рис.5.2). Парал- лельно линии пересечения зеркал на расстоянии  помещают прямо- линейный источник света
помещают прямо- линейный источник света  . Зеркала отбрасывают на эран две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников
. Зеркала отбрасывают на эран две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников 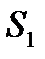 и
и 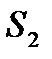 . Область, в которой волны перекрываются, называется полем интерференции.
. Область, в которой волны перекрываются, называется полем интерференции.
Б) Бипризма Френеля

| Э Рис.5. 3 |
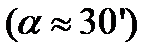 , сложенные своими основаниями (рис.5.3). Парал- лельно основанию на расстоянии
, сложенные своими основаниями (рис.5.3). Парал- лельно основанию на расстоянии  от него располагается прямо- линейный источник света S. Падающий от него пучок света вследствие преломления в бипризме разделяется на два перекрывающихся пучка, как бы исходящих из двух мнимых источников
от него располагается прямо- линейный источник света S. Падающий от него пучок света вследствие преломления в бипризме разделяется на два перекрывающихся пучка, как бы исходящих из двух мнимых источников 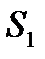 и
и 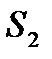 .
.
в) Метод Юнга.

| Рис.5.4 |
| Э |
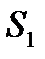 и
и 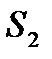 в непрозрачном экране А (рис.5.4). Первичным источ- ником света служит ярко освещенная щель S, которая параллельна щелям
в непрозрачном экране А (рис.5.4). Первичным источ- ником света служит ярко освещенная щель S, которая параллельна щелям 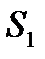 и
и 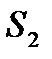 и находится от них на одина- ковом расстоянии.
и находится от них на одина- ковом расстоянии.






