Вынужденные колебания возникают в колебательной системе под действием внешней периодически изменяющейся силы. С учётом вынуждающей силы закон движения пружинного маятника запишется в виде
. (4.44)
После преобразования получим неоднородное дифференциальное уравнение, описывающее вынужденные колебания:
, (4.45)
где 
.
Общее решение данного неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения.
Общее решение однородного уравнения имеет вид
, (4.46) где 
, а A0 и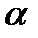 
- произвольные постоянные.
Частное решение неоднородного уравнения (4.44) имеет вид
, (4.47) где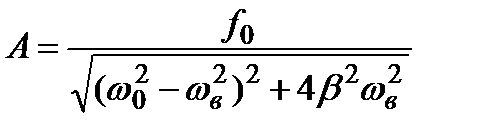 
, (4.48)
. (4.49)
Функция (4.47) в сумме с (4.46) даёт общее решение уравнения (4.45), описывающее поведение системы при вынужденных колебаниях. Слагаемое (4.46) играет значитель- ную роль в начальной стадии процесса при установлении колебаний. С течением времени его роль из-за экспонен- циального множителя всё больше уменьшается и им можно пренебречь
. Графически вынужденные колебания представлены на рисунке 4.12.
Рис. 4.12
В установившемся режиме вынужденные колебания происходят с частотой wв и являются гармоническими, амплитуда и фаза которых определяются выражениями (4.48) и (4.49).
Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При некоторой частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - резонансной частотой.
Из условия максимума функции (4.48) найдём
, (4.50)
а амплитуда колебаний при резонансе определяется из выражения
. (4.51)
Резонансные кривые при различных значениях коэф- фициента затухания представлены на рисунке 4.13. Чем меньше 
тем выше и правее лежит резонансный максимум. Если 
, то все кривые приходят к одному и тому же значению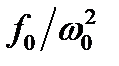 
, так называемому статическому отклоне-нию.
|
| ω в |
| ω рез |
| β3> β2> β1 |
Рис. 4.13
Резонансная амплитуда связана с добротностью колебатель- ной системы следующим соотношением
. (4.52)
Таким образом, добротность характеризует резонансные свойства колебательной системы: чем больше Q, тем острее и выше резонансная кривая.
Распространение волн в упругих средах.
Уравнение бегущей волны
Процесс распространения колебаний в упругой среде, периодический во времени и в пространстве, называется механической волной. Распространение волн не связано с переносом вещества. Частицы среды, в которой распространя- ется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесий. От одних участков среды к другим переносятся только энергия и импульс.
Различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикуляр- ных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей упругостью формы, т.е. способностью сопротив- ляться деформации сдвига. Поэтому поперечные волны могут существовать лишь в твёрдых телах. Продольные волны связаны с объёмной деформацией среды, поэтому они могут распространяться как в твёрдых телах, так и в жидкостях и в газах. Скорости распространения поперечных и продольных механических волн в твёрдых телах определяются выражениями:
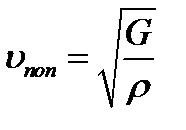, (4.53)
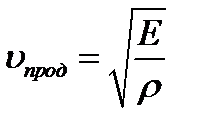, (4.54)
где G – модуль сдвига, Е – модуль Юнга.
В газообразных средах распространяется только продольная волна
, (4.55)
где R – универсальная газовая постоянная, T – абсолютная температура, μ- молекулярная масса газа.
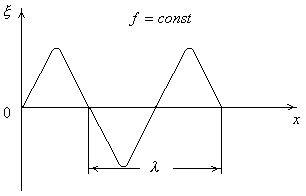
Волна называется синунусоидальной, если соответ- ствующие ей колебания частиц среды являются гармониче- скими. График зависимости смещения частиц среды 
, участвующих в волновом процессе, от расстояния x этих частиц до источника колебаний для какого-то фиксированного момента времени представлен на рисунке 4.14. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны. Длина волны l равна такому расстоянию, на которое распространяется определённая фаза волны за период, т.е.
. (4.56)
Рис.4.14
Зависимость смещения колеблющейся точки от координат и времени устанавливается уравнением волны.
В случае плоской волны, распространяющейся вдоль положительного направления оси x, уравнение имеет вид
, (4.57)
где х/υ = τ - время прохождения волной расстояния от источника (х = 0) до частицы с координатой х.
Или в стандартной форме
, (4.58)
где 
- волновое число.
Уравнение волны, распространяющейся в сторону убывания х, отличается только знаком члена kх.
Уравнение любой волны является решением некоторого дифференциального уравнения, называемого волновым. В общем случае волновое уравнение имеет вид
. (4.59)
Стоячие волны
Стоячие волны образуются при наложении двух бегущих синусоидальных волн, распространяющихся навстречу друг другу. Практически, стоячие волны возникают при отражении волн от преград.
Пусть уравнения бегущей и отражённой волны имеют вид:
.
Сложив эти уравнения, получим уравнение стоячей волны
, (4.60)
Из (4.60) следует, что в каждой точке стоячей волны происходят колебания с частотой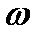 
, т.е. с частотой бегущих волн и амплитудой
, (4.61)
являющейся периодической функцией координаты х.
Точки среды, в которых амплитуда стоячей волны достигает максимального значения, называются пучностями стоячей волны.
Значения координат пучностей
, (m =1,2,3...). (4.62)
Точки среды, в которых амплитуда стоячей волны обращается в ноль, называются узлами стоячей волны. Координаты узлов определяются соотношением
. (4.63)
Расстояние между соседними узлами или соседними пучностями равно
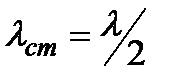, (4.64)
и называется длиной стоячей волны.
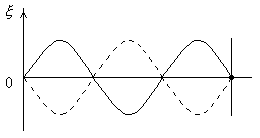
В отличие от бегущей волны, все точки которой совершают колебания с одинаковой амплитудой, но с запаздыванием по фазе, все точки стоячей волны между двумя узлами колеблются с разными амплитудами, но с одинаковы- ми фазами (синфазно). Точки, лежащие по разные стороны от узла, колеблются в противофазе. Графическое изображение стоячей волны представлено на рисунке 4.15.
Рис.4.15
В стоячей волне отсутствует перенос энергии, так как образующие эту волну падающие и отражённые волны перено- сят энергию в равных количествах и в противоположных направлениях. Полная энергия колебаний каждого элемента объёма среды, ограниченного соседним узлом и пучностью, не зависит от времени, она лишь периодически переходит из кинетической энергии, сосредоточенной вблизи пучностей, в потенциальную - вблизи узлов волны, где деформация среды достигает максимальных значений.
