Результирующее движение точки, одновременно участвующей в нескольких колебаниях, во многих случаях является колебательным. Таким образом, можно говорить о сложении нескольких колебаний в одно результирующее.
Сложение гармонических колебаний одного направления с одинаковыми частотами и различными фазами осущест- вляется с помощью вектора амплитуды, позволяющего свести сложение колебаний к сложению, векторов. Вектор амплитуды представляет собой вектор, величина которого равна амплитуде гармонического колебания, а угол между его направлением и осью X определяется начальной фазой (рис.4.5). Если привести вектор во вращение против часовой стрелки с угловой скоростью w, то его проекция на ось X будет изменяться со временем по гармоническому закону. Следовательно, гармоническое колебание может быть задано с помощью вектора амплитуды.
| ω0 |
| А1 |
| Рис.4.5 Рис.4.6 |
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты, описываемых уравнениями:
, (4.20)
. (4.21)
Представим эти колебания с помощью векторов амплитуды A1 и A2 и построим вектор A, представляющий результирующие колебания (рис.4.6).
Результирующее колебание является гармоническим с частотой ω0
, (4.22)
амплитуда которого и его начальная фаза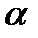 
определяются из векторной диаграммы:
, (4.23)
. (4.24)
Рассмотрим теперь два гармонических колебания, которые происходят в одном направлении, с близкими частотами ω и ω+ Δ ω (Δω<<ω). Пусть амплитуды складываемых колебаний одинаковы А1=А2= А, а начальные фазы колебаний α1= α2 = 0.
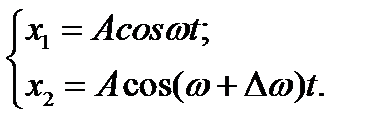(4.25)
Результирующее колебание x = x1+ x2, т.е.
x = А cosωt + А cos(ω+ Δ ω)t =
= 
(4.26)
Учитывая что Δ ω << ω, получим
. (4.27)
Так как 
изменяется значительно медленней, чем cosωt, результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда которого медленно
изменяется также по гармоническому закону с частотой 
. Такие колебания называются биениями (рис.4.7).
| Х |
| t |
Рис.4.7
Уравнение биений имеет вид
(4.28)
Амплитуда колебаний равна 
, частота пульса- ций амплитуды (биений), равна разности частот складываемых колебаний (см. рис.4.7), а период биений .
4.1.5. Сложение взаимно перпендикулярных
колебаний. Фигуры Лиссажу
Пусть колебания одинаковой частоты совершаются вдоль взаимно перпендикулярных координатных осей X и Y. Выберем начало отсчёта времени так, чтобы начальная фаза первого колебания была равна нулю. Запишем уравнения колебаний таким образом
, (4.29)
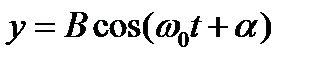, (4.30)
где 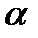- разность фаз складываемых колебаний.
Исключив из данных уравнений параметр t, получим уравнение траектории результирующего колебания.
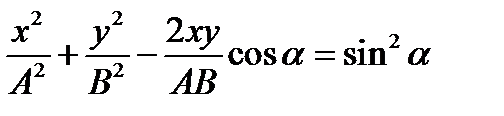. (4.31)
Уравнение (4.31) представляет собой уравнение эллипса, произвольно ориентированного относительно координатных осей X и Y.
Рассмотрим частные случаи:
1) При 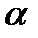= 0 уравнение (4.31) принимает вид
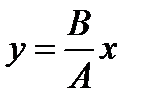. (4.32)
Колеблющаяся точка переме- щается по прямой, причём расстоя- ние от начала координат изменяется по закону.
| В -А А х -В |
| y |
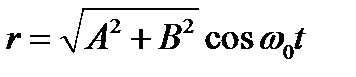. (4.33)
| В -А +А х -В |
| y |
2) При 
результирую- щее колебание так же является гармоническим и совершается вдоль прямой, описываемой уравнением
. (4.34)
| y B |
| - π/2 х +π/2 |
| - A A -B |
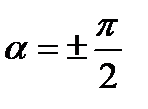уравне- ние (4.31) становится уравне- нием эллипса, приведённого к координатным осям
. (4.35)
Направление обхода элипса определяется знаком перед π/2. При равенстве амплитуд эллипс вырождается в окружность.
При сложении взаимноперпендикулярных гармони- ческих колебаний с кратными частотами, траектории движения точки имеют вид сложных кривых – фигур Лиссажу, вид которых зависит от соотношения частот, и разности фаз складываемых колебаний.
Например, при сложения двух колебаний с частотами ω и 2 ω и разностью фаз Δφ1 =0 и Δφ2 = π/2, соответствующие фигуры Лиссажу показаны на рис.4.8 и рис.4.9.
| y В |
| х -А +А -В |
| y В |
| х -А +А -В |
| Рис.4.8 |
| Рис.4.9 |
.
По виду фигуры Лиссажу можно определить соотношение частот и разность фаз складываемых колебаний.
