| Рис. 5.24 |
| луч |
|
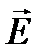 и магнитного
и магнитного  полей происходят перпендикулярно направлению распространения волны. Вместе с тем световые волны не обнаруживают ассиметрии относительно направле- ния распространения, так как они слагаются из множества цугов волн, испускаемых отдельными атомами светящегося тела. Плоскость колебаний светового вектора для каждого цуга ориентирована случайный образом. Поэтому в результирую- щей волне колебания
полей происходят перпендикулярно направлению распространения волны. Вместе с тем световые волны не обнаруживают ассиметрии относительно направле- ния распространения, так как они слагаются из множества цугов волн, испускаемых отдельными атомами светящегося тела. Плоскость колебаний светового вектора для каждого цуга ориентирована случайный образом. Поэтому в результирую- щей волне колебания 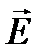 различных направлений представлены с равной вероятностью, такой свет называется естественным (рис. 5.24).
различных направлений представлены с равной вероятностью, такой свет называется естественным (рис. 5.24).
Свет, в котором колебания каким-либо образом упорядочены, называется поляризованным.
Если колебания светового вектора происходят только в одной плоскости, свет называется плоско - поляризованным. Плоскость в которой колеблется световой вектор 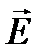 называется плоскостью колебаний, а перпендикулярная к ней плоскость, в которой колеблется вектор
называется плоскостью колебаний, а перпендикулярная к ней плоскость, в которой колеблется вектор  , называется плоскостью поляризации.
, называется плоскостью поляризации.
Свет, в котором колебания одного направления преобла- дают над колебаниями других направлений, называется частично - поляризованным. Такой свет можно рассмат- ривать как смесь естественного и плоскополяризованного. Если пропустить частично поляризованный свет через поляризатор, то при вращении прибора вокруг направления луча, интенсивность прошедшего света будет изменяться от I max до I min , причём переход от одного из этих значений к другому будет совершаться при повороте на угол  . За один полный оборот два раза будет достигаться максимальное и два раза минимальное значение интенсивности.
. За один полный оборот два раза будет достигаться максимальное и два раза минимальное значение интенсивности.
Степенью поляризации называют выражение
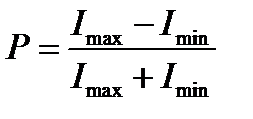 . (5.54)
. (5.54)
Для плоскополяризованного света Imin= 0 и P =1, для естествен- ного света 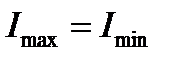 и Р = 0.
и Р = 0.
Плоскополяризованный свет можно получить из естественного с помощью прибора, называемого поляриза- тором. Он пропускает колебания, параллельные плоскости поляризатора, и полностью задерживает колебания, перпендикулярные этой плоскости.
Пусть на поляризатор падает плоскополяризованнный свет амплитуды 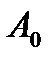 и интенсивности
и интенсивности  (рис.5.25). Сквозь прибор пройдет составляющая колебания с амплитудой
(рис.5.25). Сквозь прибор пройдет составляющая колебания с амплитудой
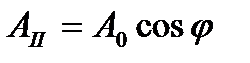 , (5.55)
, (5.55)
где 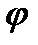 - угол между плоскостью колебаний и плоскостью поляризатора.
- угол между плоскостью колебаний и плоскостью поляризатора.
Следовательно интенсивность света  , вышедшего из анализатора, пропорциональна квадрату амплитуды
, вышедшего из анализатора, пропорциональна квадрату амплитуды  и определяется выражением
и определяется выражением
| Рис.5.25 |
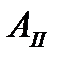
|
| плоскость поляризатора |
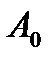
|
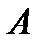
|
|
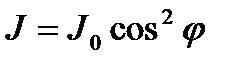 , (5.56)
, (5.56)
которое называется законом Малюса.
Если на поляризатор падает естественный свет, то все значения 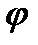 являются равновероятными. Поэтому доля света, проходящего через поляризатор, будет равна среднему значению
являются равновероятными. Поэтому доля света, проходящего через поляризатор, будет равна среднему значению 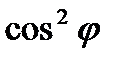 , т. е. равна 1/2.
, т. е. равна 1/2.
 .
.






