Пример 1. Частица совершает гармонические колебания вдоль оси х около положения равновесия x =0, частота колеба- ния w0 = 4с-1. В некоторый момент времени координата частицы x 0 = 25 см и ее скорость u0 = 100 см/с. Найти координату x и скорость u частицы через t = 2,4 с после этого момента.
Решение
Запишем уравнение гармонических колебаний частицы в виде:
x = Acos(w0t + j0), (1)
тогда уравнение скорости будет иметь вид:
(2)
Для нахождения параметров данных уравнений воспользуемся начальными условиями. При t = 0 имеем:
х0 = Аcosj0,
u0 = -Аw0sinj0,
откуда 
и φ0= -p/4,
.
Координата и скорость частицы u в момент времени t = 2,4 с найдутся из уравнение (1) и (2):
х = - 29 см, u = -81 см/с.
Пример 2. Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т = 0,6 с и амплитудой А = 10 см. Найти среднюю скорость точки за время, в течении которого она проходит путь А/2:
а) из положения равновесия; б) из крайнего положения.
Решение
Выберем за начало отсчета времени момент, когда точка проходит положение равновесия. Тогда уравнение колебаний имеет вид:
х = Аsinw0t.
Исходя из этого уравнения определим момент времени t1, соответствующий смещению точки х = А/2. Имеем:
,
откуда t1 = T / 12.
Значение средней скорости точки при ее движении из положения равновесия определяется из формулы:
uср1 = 100 см/с.
Время движения точки из крайнего положения до половины амплитуды будет равно:
.
С учетом этого:
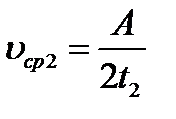; uср2 = 50 см/с.
Аналогичные результаты могут быть получены при использовании формулы:
Пример 3. Найти амплитуду и начальную фазу результирующего колебания, возникающего при сложении двух одинаково направленных колебаний, выражаемых уравнениями: х1 = 3cos(wt + p/3) см, х2 = 8sin(wt + p/3) см.
Написать уравнение результирующего колебания.
Решение
Вначале, используя тригонометрические формулы, приведем уравнение второго колебания к виду
х2 = 8 cos(wt - p/6) см.
| А1 0 φ 1 х φ2 А А2 |
,
где Dj = j2 - j1.
Произведя вычисления, найдем А = 8,5 см. Тангенс начальной фазы результирующего колебания определится из рисунка
, откуда j = - 0.2 рад.
Уравнение результирующего колебания запишется в виде:
0
l lc
c
m3
х =8,5cos(wt – 0.2) см. m2
Пример 4. На концах тонкого стержня длиной l = 1 м и массой m1 = 0,4 кг укреплены шарики малых размеров массами m2 = 0,2 кг и m3 = 0,4 кг. Стержень колеблется около горизонталь- ной оси, перпендикулярной стержню и проходящей через его середину. Опреде- лить период колебаний, совершаемых стержнем.
Решение
Стержень с шариком (см. рис.) представляет собой физический маятник, период колебаний которого определяется формулой
,
где I - момент инерции маятника относительно оси колебаний; m – масса; l c – расстояние от центра масс маятника до оси.
Принимая шарики за материальные точки, общий момент инерции маятника определяем выражением
I = (1/12) m1l 2 + m2 (l /2)2 + m3 (l /2)2 = (1/12) l 2(m 1 + 3 m 2 + 3 m 3),
I = 158 кгּ м2.
Масса маятника m = m1 + m2 + m3 = 0,9 кг.
Расстояние l c от оси маятника до его центра масс равно
Произведя вычисления, найдем l c = 5,55 см, Т = 11,2 с.
Пример 5. Тело массой m = 5 г совершает затухающие колебания. В течении времени t =50 с тело потеряло 60 % своей энергии. Определить коэффициент сопротивления r.
Решение
Энергия тела, совершающего колебания, определяется по формуле
E = mA2w2/2.
Учитывая зависимость амплитуды затухающих колебаний от времени A = А0 е- b t,
получим 
или
E = E0 е -2b t, (1)
где 
– энергия тела в момент времени t = 0.
К моменту времени t =50 с тело потеряло 60 % своей перво- начальной энергии, следовательно,
E = 0,4 E0. (2)
Приравнивая (1) и (2), сокращая на E0 и, логарифмируя обе части равенства, найдем:
ln 2,5 = 2 bt.
Отсюда выражаем b:
b = (ln 2,5)/2 t. (3)
С другой стороны, b = r/2m. (4)
Из сравнения (3) и (4) получим r = (m ln2,5)/ t
После подстановки числовых значений найдем
r = 9,16×10-5 кг/с.
Пример 6. Тело массой m = 10 г совершает затухающие колебания с максимальным значением амплитуды 7 см, начальной фазой, равной нулю, коэффициентом затухания, равным 1,6 с-1. На это тело начала действовать внешняя периодическая сила, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид x =5sin(10pt - 0,75p) см. Найти: 1) уравнение свобод- ных колебаний; 2) уравнение внешней периодической силы.
Решение
Уравнение свободных затухающих колебаний имеет вид
х = А0 е - bt sinw t, (1)
где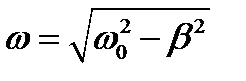 
- частота затухающих колебаний; w0 – собствен ная частота колебаний; b - коэффициент затухания.
По условию сдвиг фаз j между собственными и вынужден- ными колебаниями равен – 3p/4; следовательно, tg (-3p/4) = 1.
С другой стороны,
Из равенства
cледует 
(2)
У нас wв = 10p, b = 1,6 с-1. Подставляя эти значения в (2), получим, что b2 << w02, получим, что частота w затухающих колебаний равна частоте w0 собственных колебаний. Следовательно, уравнение свободных затухающих колебаний примет вид
х = 7 e -1,6 t sin 10,5 w p t см.
Уравнение внешней периодической силы
F = F0 sinw t. (3)
Амплитудное значение вынуждающей силы
(4)
После подстановки числовых значений получаем F0 =
= 72 мН. С учетом этого уравнение внешней периодической силы будет иметь вид
F = 72 sin 10 p t мН.
Пример 7. Сила, действующая на материальную точку, изменяется по гармоническому закону F = F0 sinw t. В началь- ный момент времени скорость точки равна нулю. Как с течением времени изменяется скорость и положение точки?
Решение
По второму закону Ньютона
, или 
(1)
Отсюда 
тогда скорость колеблющейся
точки 
(2)
Обозначая 
, перепишем (2) в виде
График изменение скорости представлен на рис.1
Если начальное положение точки принять за начало координат, то координата точки в любой момент времени определяется выражением
Таким образом, движение точки под действием периодической силы является поступательным с периодиче- ским возрастанием скорости от 0 до 2 um, а затем снова до 0 (рис. 2.).
| x |
| 0 T t |
| υ 2υm |
| T 2T t |
Рис. 1 Рис. 2
Пример 8. Плоская волна распространяетсявдоль прямой со скоростью υ =20 м/с. Две точки, находящиеся на этой прямой на расстоянии х1 =12 м и х2 =15 м от источника волн, колеблются с разностью фаз Δ φ = 0,75 π. Найти длину волны λ, написать уравнение волны и найти смещение указанных точек в момент t = 1,2 с, если амплитуда колебаний А = 0,1 м.
Решение
Точки, находящиеся друг от друга на расстоянии, равном длине волны λ, колеблются с разностью фаз, равной 2 π; точки, находящиеся друг от друга на любом расстоянии Δ x, колеблются с разностью фаз, равной
.
Решая это равенство относительно λ, получим
. (1)
Подставляя числовые значения величин, входящих в выражение (1), получим λ = 8 м.
Для того, чтобы написать уравнение плоской волны, надо ещё найти циклическую частоту ω. Так как ω=2π/T (T = λ/υ – период колебаний), то
.
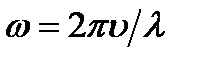Произведя вычисления, найдём
Зная амплитуду колебаний А, циклическую частоту ω скорость распространения волны υ, можно написать уравнение плоской волны для данного случая
(2)
где А = 0,1 м, ω= 5 π с-1, υ= 20 м/c.
Чтобы найти смещение указанных точек y, достаточно в уравнение (2) подставить значения t и х:
y1 = - 0,1 м; y2 = 7,1 см.
Пример 9. Омическое сопротивление контура 
Ом, индуктивность 
, ёмкость 
. Определить силу тока в контуре в момент времени 
, если при 
заряд на конденсаторе 
, а начальная сила тока равна нулю.
Решение
Общий вид уравнения затухающих колебаний в контуре запишем в виде:
, (1)
где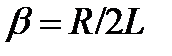 
,
.
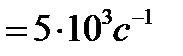Начальную фазу 
и амплитудное значение заряда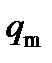 
определим из начальных условий. Учитывая, что при 
, получаем
. (2) Найдём выражение для силы тока
. (3)
Так как при 
и I = 0,получаем
.
Откуда 
и 
. Наконец, из (2) находим
.
С учётом найденных параметров уравнения (3) определим силу тока в контуре в момент времени
, 
.
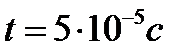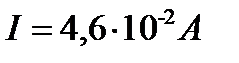| R |
| C |
| L |
| E |
Пример 10. В цепи, состоящей из последовательно соединённых резис- тора 
, катушки индуктив- ностью 
и конденсатора ёмкостью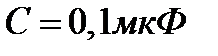 
, действует синусо- идальная ЭДС. Определите частоту 
ЭДС, при которой в цепи наступит резонанс. Найти действующие значения силы тока I и напряжений UR, UL, UC на всех элементах цепи при резонансе, если при этом действующее значение ЭДС 
.
Решение
Под действием переменной ЭДС в цепи 
установятся вынужденные колебания. При этом амплитудные значения тока 
и ЭДС 
связаны соотношениями
.
В соответствии с формулами, связывающими амплитуд- ные и действующие значения токов и напряжений (
, 
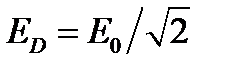), данное соотношение имеет аналогичный вид и для действующих значений:
.
Максимальному току при резонансе 
соответствует такое значение 
,при котором выполняется условие
, откуда 
.
При этом сила тока 
. Зная силу тока 
, найдём действующие значения напряжения на каждом из элементов контура. В соответствии с законом Ома для каждого из участков получим:
,
,
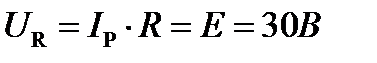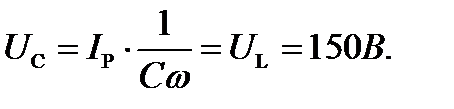
Равенство 
следует из равенства 
при резонансе.
5. ВОЛНОВАЯ ОПТИКА
5.1. Световая волна. Когерентность и монохроматичность световых волн
Свет представляет собой электромагнитную волну, в которой происходят колебания векторов напряженности электрического и магнитного полей. Однако, как показывает опыт, различные действия света (физиологическое, фото- химическое, фотоэлектрическое и др.) вызываются колеба- ниями электрического вектора. Поэтому в дальнейшем этот вектор будем называть световым вектором, а плоскую световую волну описывать лишь одним уравнением
(5.1)
где A -амплитуда светового вектора, 
- частота колебаний, 
- волновое число.
Длины и частоты видимого света лежат в пределах 
и 
.
Скорость распространения света в вакууме есть одна из важнейших констант физики и равна 
. В других средах она меньше и определяется по формуле
, (5.2)
где n- показатель преломления среды.
Для всех прозрачных сред 
, поэтому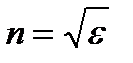 
.
При переходе света из одной среды в другую частота колебаний ν в световой волне сохраняется, но длина волны изменяется
. (5.3)
Средний по времени световой поток через единицу поверхности площадки, перпендикулярной к направлению распространения волны, носит название интенсивности света. Интенсивность света пропорциональна квадрату амплитуды световой волны
(5.4)
где n -показатель преломления среды.
Световая волна, описываемая уравнением (5.1), называется монохроматической. Однако, ни один реальный источник (исключая лазерный) не даёт строго монохромати- ческого света. Реальное излучение содержит в себе ни одну определённую частоту, а некоторый набор частот. Чем уже интервал частот ∆ν, тем более монохроматичным оно является.
Причина немонохроматичности излучения всякого источника, кроме лазерного, заключается в самом механизме испускания света. Излучение светящегося тела слагается из волн, испускаемых атомами. Излучение отдельного атома продолжается τ ≈ 
. За это время образуется цуг протяжён- ностью 
. Одновременно излучает большое количество атомов. Возбуждаемые ими цуги, налагаясь друг на друга, образуют световую волну. Фаза реальной световой волны изменяется с течением времени, поскольку излучение одной группы атомов сменяется излучением другой. Время, за которое случайные изменения фазы в световой волне достигают значение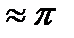 
, называют временем когерентности. За это время волна становится некогерентной к самой себе. Таким образом, время когерентности гораздо меньше времени излучения одного цуга.
Интерференция света
