Идеализированные системы, в которых колебания возникают за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий и описыва- ются уравнением (4.4), называются гармоническими осцил- ляторами. Примерами гармонических осцилляторов являются пружинный, физический и математический маятники. Колеба- ния, возникающие в таких системах при отсутствии сил трения, называются собственными гармоническими колеба- ниями.
Математическим маятником называют идеализи- рованную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке (рис.4.3).
| l |
| j |
| o |
| M |
|
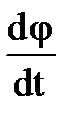
| mg |
| c •· P 2 α P1 P |
| O |
| lс |
| lпр |
| α |
| o’ |
Рис.4.3 Рис.4.4
При отклонении от положения равновесия на некоторый угол 
математический маятник начинает совершать свобод- ные колебания. В случае малых колебаний 
, диф- ференциальное уравнение колебаний математического маятника имеет вид
, (4.10)
где 
; 
– длина математического маятника; 
– ускорение свободного падения.
Общее решение этого дифференциального уравнения имеет вид
, (4.11) где 
и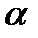 
– постоянные, определяемые начальными условиями возбуждения колебаний.
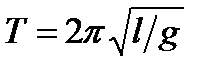. (4.12)
Видно, что период 
зависит только от длины маятника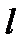 
, ускорения силы тяжести 
и не зависит от его массы.
Физический маятник – любое тело, подвешенное в точке, лежащей вне его центра тяжести(рис 4.4).
Докажем, что маятник, отклоненный на малый угол a от положения равновесия, будет совершать гармонические колебания. Обозначим через I момент инерции маятника относительно оси О, перпендикулярной плоскости чертежа (рис.4.4). Пусть точка С является центром тяжести. Силу тяжести P = mg можно разложить на две составляющие, одна из которых P 2 уравновешивается реакцией опоры.
Под действием другой составляющей
P1 = P×sina = mg sin α (4.13)
маятник приходит в движение. Из основного закона динамики вращательного движения имеем
I e = - m g lc sina, (4.14)
где 
, (4.15) угловое ускорение, lc = СО – расстояние от точки подвеса до центра тяжести.
Знак минус выбран потому, что действующая сила направлена в сторону, противоположную положительному направлению отклонения маятника, т.е. стремится вернуть его в положение равновесия. При малых отклонениях можно считать, что sin a» a, поэтому
Р1» m g a. (4.16)
Подставив (4.15) и (4.16) в (4.14), получим
. (4.17)
Полученное дифференциальное уравнение является уравнением гармонического колебательного движения. Частота и период колебаний определяются из формул
(4.18)
Величина 
называется приведённой длинойфизического маятника, она численно равна длине математического маятника с периодом колебаний, равным периоду колебаний данного физического маятника.
Таким образом, период и частота колебаний физического маятника определяются выражениями
. (4.19)
