Дифракция плоской волны (дифракция Фраунгофера) на узкой щели

 

Щелью называется прямоугольное отверстие, имеющее незначительную ширину и практически бесконечную длину. Пусть монохроматическая световая волна падает по нормали к плоскости щели шириной b (рис. 5.18). При этом все точки фронта волны, совмещённого с плоскостью щели, будут колебаться с одинаковой фазой.

A B   φ   φ D

Э M O

b

Л

 

Рис. 5.18

 

Параллельный пучок света, пройдя через щель, дифрагирует под разными углами в правую и левую сторону от первоначального направления. Линза Л собирает парал- лельные пучки дифрагированных лучей в соответствующих точках экрана Э, расположенного в её фокальной плоскости. Недифрагирующие лучи соберутся в центре экрана в точке О и здесь всегда будет максимум освещённости. Лучи, дифраги- рующие влево под углом 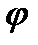, соберутся в точке M. Освещенность этой точки зависит от разности хода между крайними лучами:

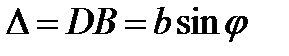. (5.43)

Найдём условие максимума и минимума дифракции с помощью метода зон Френеля. Разобьём щель АВ на зоны, имеющие вид полос, параллельных ребру щели, так чтобы расстояние от двух соседних полос до точки наблюдения М различалось на . При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами. Результат интерференции определяется тем, сколько зон укладывается на ширине щели. При четном числе зон в точке наблюдения будет минимум дифракции, при нечётном – максимум. Чётному числу зон Френеля на ширине щели соответствует чётное число на оптической разности хода (рис. 5.19).

Рис. 5,19

Поэтому условия дифракционного минимума и максимума соответственно будут иметь вид:

(5.44)   (5.45)     5.4155 (2.42)

Знак (–) в этих выражениях соответствует лучам, распространяющимся под углом () относительно направле- ния падающих лучей.

На рис. 5.20 представ- лен график распределения интенсивности света на экране. Основная часть световой энергии сосредо- точена в центральном максимуме. Примерно 5% энергии приходится на первые и 2% – на вторые максимумы.

Рис. 5.20

 

 

5.3.6. Дифракция Фраунгофера на решётке

 

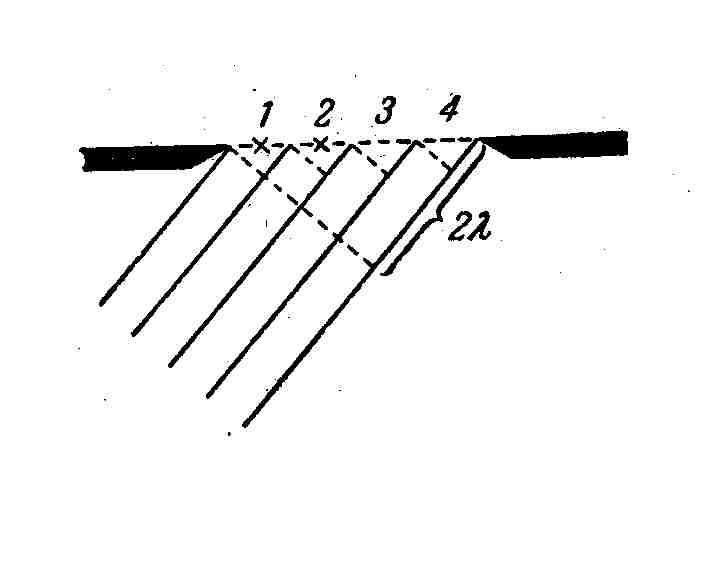
Дифракционная решётка представляет собой систему, состоящую из большого числа одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделённых непрозрачными промежутками, равными по ширине (рис. 5.21)

 

в а d

φ Δ=dsinφ φ

М

F

 

 

Рис.5.21

 

Расстояние между соседними щелями называется периодом дифракционной решётки:

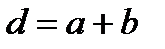, (5.46)

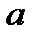где - ширина щели, - ширина непрозрачного промежутка.

При освещении решётки монохроматическим светом дифракционная картина на экране усложняется (по сравнению с одной щелью) за счет интерференции света от различных щелей.

Пусть монохроматическая волна падает на поверхность решётки по нормали (рис. 5.21). Колебания во всех точках щелей происходят в одной фазе, так как они принадлежат одной волновой поверхности. Найдём амплитуду световой волны в точке M экрана, в которой собираются лучи от всех щелей, дифрагированные под углом .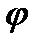

В одном и том же направлении все щели излучают свет одинаково, то есть все амплитуды 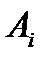равны. Колебания от сходственных точек соседних щелей в точке M будут усиливать друг друга, если на их разности хода будет укладываться в соответствии (5.11) чётное число полуволн или целое число длин волн.

Таким образом, положение главных максимумов определяется формулой

, (5.47)

где 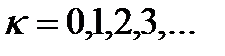определяет порядок максимума.

Амплитуда колебаний в этой точке экрана равна

,

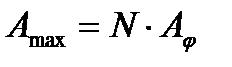где 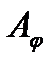- амплитуда колебания, посылаемого одной щелью под углом .

Для направлений, удовлетворяющих условию

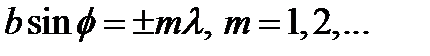, (5.48)

которое является условием минимума дифракции для одной щели, все 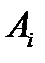равны нулю. Поэтому амплитуда результирую- щего колебания в соответствующей точке экрана также равна нулю. Таким образом, условие (5.48) минимума для одной щели является также условием минимума дифракции для решётки.

Кроме главных минимумов, определяемых условием (5.48), в промежутках между соседними главными максимумами имеется по (N-1) - му добавочному минимуму. Эти минимумы возникают в тех направлениях, для которых колебания от отдельных щелей взаимно погашают друг друга. Направление добавочных минимумов определятся условием

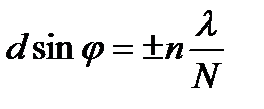, (5.49)

где 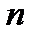принимает все целочисленные значения () кроме .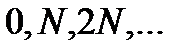

Между дополнительными минимумами располагаются слабые вторичные максимумы. Число таких максимумов, находящихся в промежутке между соседними главными максимумами, равно (N -2).

Дифракционная картина, полученная от решётки с N = 4 и 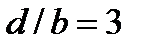, изображена на рис. 5.22.

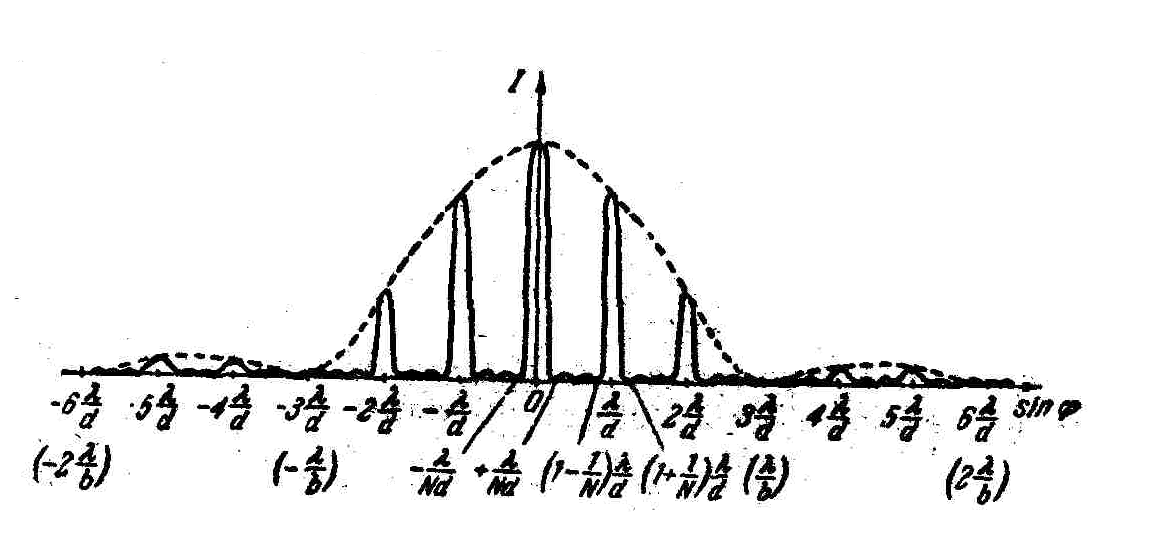
Рис. 5.22

При пропускании через решётку белого света все максимумы, кроме центрального разложатся в спектр, фиолетовый конец которого расположен к центру дифракцион- ной картины, красный – наружу. Дифракционная решётка является спектральным прибором, предназначенным для анализа спектрального состава исследуемого излучения. Качество спектрального прибора характеризуется дисперсией и разрешающей силой.

Дисперсия характеризует ширину спектра, получаемого дифракционной решёткой. Различают угловую и линейную дисперсию. Угловая дисперсия определяет угловое расстояние 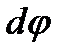между двумя спектральными линиями, отличающимися по длине волны на :

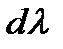(5.50)

Линейная дисперсия определяет линейно расстояние в фокальной плоскости между этими линиями

(5.51)

где F – фокусное расстояние линзы, d – период дифракцион- ной решётки, к – порядок максимума.

Из представленного выражения следует, что дисперсия обратно пропорциональна периоду решётки и прямо пропорциональна порядку спектра.

Разрешающая сила характеризует свойства дифракцион- ной решётки разделять излучения близкие по длине волны и определяется выражением

, (5.52)

где - минимальное различие в длине волны, которое может быть обнаружено, N – число щелей дифракционной решётки.

Таким образом, разрешающая сила дифракционной решётки пропорциональна порядку спектра и числу щелей.

 

5.3.7. Дифракция на пространственной (объёмной) решётке

 

В качестве пространственных решёток могут быть использованы кристаллы, в которых атомы располагаются в правильном порядке на определённом расстоянии (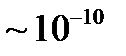 м) друг от друга по трём координатным осям. При прохождении электромагнитных волн через кристалл, атомы, расположенные в узлах кристаллической решётки, становятся источниками вторичных волн, интерференция которых и приводит к возникновению дифракционной картины.

Для получения дифракционной картины необходимо, чтобы период структуры 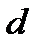был больше длины волны . Видимый свет этому условию не удовлетворяет. Для дифракции на пространственной решётке нужны рентгеновские лучи.

Проведем через узлы кристаллической решётки атом- ные плоскости. Пучок параллельных рентгеновских лучей падает на кристалл под углом скольжения (рис. 5.23) и отражается под таким же углом.

Для того чтобы лучи, отраженные от соседних плоскостей усиливали друг друга, разность хода должна быть кратна целому числу длин волн, т.е. 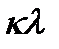. Следовательно максимум интенсивности дифрагированных лучей наблюдается под углами , которые удовлетворяют условию:

Q

d   d

. (5.53)

 

 

 

Рис.5.23

 

Формула (5.53) была получена русским учёным Г.В. Вульфом и английским учёным У.Л. Брэггом и называется формулой Вульфа–Брэгга.

Дифракция рентгеновских лучей от кристаллов используется для исследования спектрального состава рентгеновского излучения (рентгеновская спектроскопия) и для изучения структуры кристаллов (рентгеноструктурный анализ).

 

Поляризация света