Для осуществления вынужденных электромагнитных колебаний нужно включить последовательно с элементами контура источник переменного напряжения, изменяющегося по гармоническому закону.
U = U0 cos ωв t. (4.82)
| Рис. 4.19 |
| C |
| R |
| L |
| ~ U |
. (4.83)
Произведя преобразования, получим стандартное диффе- ренциальное уравнение вынуж- денных электромагнитных колебаний.
. (4.84)
В случае установившихся колебаний решение дифферен- циального уравнения имеет
q = q0 cos(ωв t + ψ), (4.85)
где ψ – сдвиг фаз между зарядом на обкладках конденсатора и переменной ЭДС.
Следовательно, в установившемся режиме, вынужденные колебания происходят с частотой вынуждающего напряжения ωв и являются гармоническими, амплитуда и фаза которых определяется выражениями
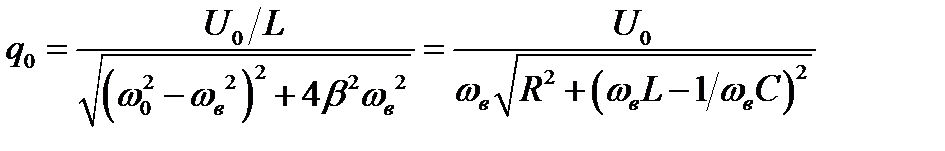, (4.86)
. (4.87)
Резонансные кривые для заряда (напряжения на конденсаторе) аналогичны резонансным кривым при механических колебаниях (см. рис.4.13), а резонансная частота определяется по формуле (4.50).
Продифференцировав (4.85) по t, найдем силу тока в контуре
I = - q0 ωв sin(ωв t + ψ) = I0 cos(ωв t + ψ + π/2),
где I0 = q0 ωв – амплитуда тока.
Запишем это выражение в виде
I = I0 cos(ωt – φ), (4.88)
где φ = -(ψ + π/2) – сдвиг фаз между током и приложенным напряжением.
Тогда в соответствии с (4.86) и (4.87)
, (4.89)
. (4.90)
Из формулы (4.90) следует, что ток отстаёт по фазе от вынуждающего напряжения в том случае, когда 
, и опережает, когда 
. При условии 
сдвиг фаз равен нулю, а амплитуда тока достигает максимального значения.
Разделив выражение (4.85) на емкость, получим напряжение на конденсаторе
, (4.91)
где
. (4.92)
Умножив производную функции (4.88) на L, получим напряжение на индуктивности:
(4.93)
где 
. (4.94)
Сопоставление формул (4.88), (4.91) и (4.93) показывает, что напряжение на емкости отстает по фазе от силы тока на π/ 2, а напряжение на индуктивности опережает ток на π /2.
Напряжение на активном сопротивлении изменяется в фазе с током. Фазовые соотношения можно представить очень наглядно с помощью векторной диаграммы (рис. 4.20).
| U |
| UC |
| w в LI0 |
| I0/ wв C |
| UL |
| UR |
| I0R |
|
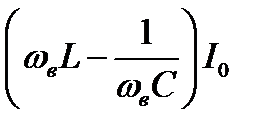
| φ |
| Рис.4.20 |
Резонансная частота для заряда и напряжения на конденса- торе равна
. (4.95)
Резонансные кривые для силы тока изображены на рис. 4.22. Амплитуда силы тока имеет максимальное значение при 
.
| R1 < R2 < R3 R1 R2 R3 |
| U 0 |
| 0 ωрез ω0 ω |
| U co |
Рис. 4.21
| w0 |
| R |
| R |
| R |
| R |
| R |
| R |
| < |
| < |
| w |
| I0 |
| Рис. 4.22 |
Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура
. (4.96)
При ω →0, I = 0, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.
Резонансные свойства контура характеризует доброт- ность Q, которая показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение, т.е.
(4.97)
При малых затуханиях ω рез ≈ ω0 и
(4.98)
Таким образом, добротность обратно пропорциональна активному сопротивлению контура.
Добротность контура определяет остроту резонансных кривых. На рис. 4.23 изображена одна из резонансных кривых для силы тока в контуре. Частоты ω1 и ω2 соответствуют току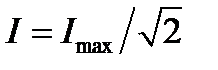 
.
| Рис.4.23 |
Относительная ширина резонансной кривой 
равна величине обратной добротности контура, т. е.
(4.99)
| Рис. 4.23 |
Явление резонанса используют для выделения из сложного напряжения, равного сумме нескольких синусо- идальных напряжений, нужной составляющей. Настроив контур (посредством изменения R и C) на требуемую частоту wi, можно получить на конденсаторе напряжение в Q раз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляю- щими, будет слабым. Таким образом, осуществляется, например, настройка радиоприёмника на нужную длину волны.
Электромагнитные волны
Существование электромагнитных волн вытекает из уравнений Максвелла для электромагнитного поля (3.1, 3.4.--3.6.). Если возбуждать с помощью колеблющихся зарядов переменное электромагнитное поле, то возникает последо- вательность взаимных превращений электрического и магнитного полей, распространяющихся в окружающем пространстве от одной точке к другой. Этот периодический во времени и пространстве процесс и представляет собой электромагнитную волну.
Фазовая скорость электромагнитных волн в различных средах определяется формулой
, (4.100)
где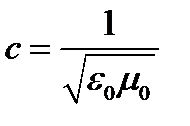 
- скорость электромагнитных волн в вакууме.
Электромагнитные волны являются поперечными, поскольку векторы 
и 
напряжённости электрического и магнитного полей взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости распростра- нения волны, образуя правовинтовую систему (рис.4.24). При этом векторы и 
колеблются в одинаковых фазах, а их мгновенные значения в любой точке связаны соотношением
. (4.101)
Уравнения плоской монохроматической электромагнитной волны имеют вид
, (4.102)
, (4.103)
где ω- частота волны, k = ω/υ = 2π/λ – волновое число, α-
начальная фаза колебаний.
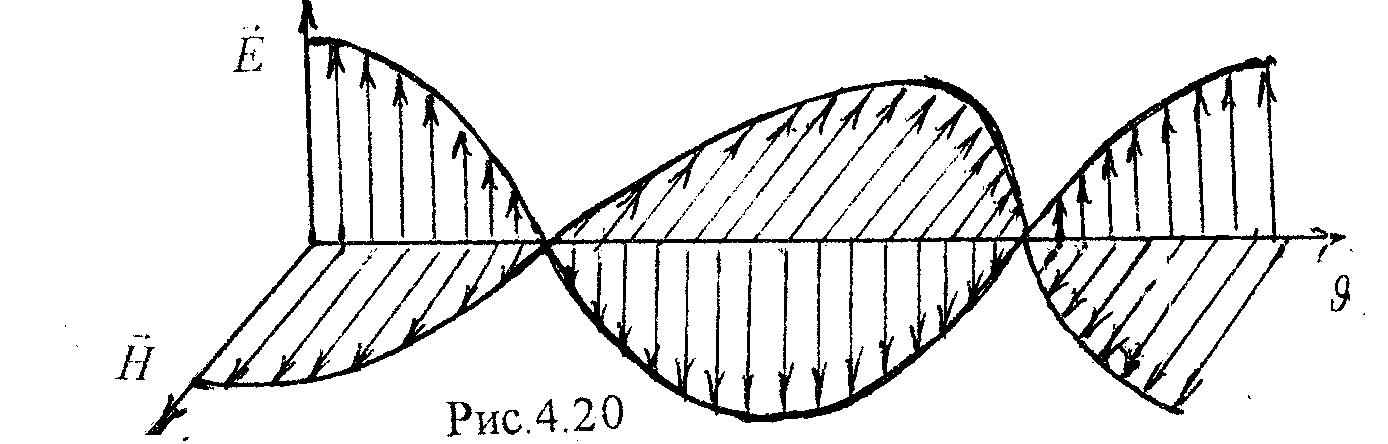
| Рис.4.24 |
Электромагнитные волны переносят энергию. Объёмная плотность энергии электромагнитной волны равна сумме объёмных плотностей энергии электрических и магнитных полей, т.е.
. (4.104)
Интенсивность монохроматической электромагнитной волны, равная энергии переносимой за единицу времени через единичную площадку, перпендикулярную скорости распро- странению волны, определяется выражением
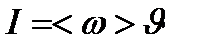, (4.105)
где < ω > - среднее за период значение объёмной плотности энергии.
Поскольку < ω > прямо пропорционально квадрату амплитуды напряжённости электрического поля, то и
I ~ А2. (4.106)
Простейшей системой, излучающей электромагнитные волны, является электромагнитный диполь, момент 
которого изменяется с течением времени. Интенсивность излучения диполя в различных направлениях характеризуется полярной диаграммой направленности излучения диполя (рис.4.25).
Из этой диаграммы видно, сильнее всего диполь излучает в направлении перпендикулярном его оси. Вдоль своей оси диполь не излучает совсем. Мощность излучения диполя пропорциональна четвёртой степени частоты колебаний.
| φ |
Рис.4.25
В зависимости от частоты (или длины волны λ = с/ν), а также способа излучения и регистрации различают несколько видов электромагнитных волн: радиоволны (9-ти диапазонов), световые волны, рентгеновское и γ – излучение.
