Линейные модели обычно применяются для анализа простых взаимосвязей между экономическими показателями. Однако в ряде случаев экономические соотношения имеют более сложный характер и их представление в виде линейной зависимости не всегда возможно, а часто и не корректно.
Однако часто нелинейные связи между объясняющими и объясняемой переменной можно с помощью определенных преобразований свести к линейным.
К таким нелинейным связям в частности относятся:
1) Нелинейные регрессии относительно объясняющих переменных Хi, но линейные по оцениваемым параметрам  i .
i .
а) Y =  0 +
0 +  1 Х +
1 Х +  2 Х 2 + …+
2 Х 2 + …+  m Хm +
m Хm + 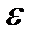 - степенной полином.
- степенной полином.
б) Y =  0 +
0 +  1
1  +
+ 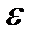 - равносторонняя гипербола.
- равносторонняя гипербола.
2) Регрессии нелинейные по оцениваемым параметрам  i .
i .
а) Y = А  - показательная функция.
- показательная функция.
б) Y = A  - степенная функция.
- степенная функция.
в) Y = 
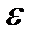 - экспоненциальная функция.
- экспоненциальная функция.
Нелинейности первого вида приводятся к линейным регрессиям с помощью преобразования объясняющих переменных (введением новых переменных).
Примеры.
Y =  0 +
0 +  1 Х +
1 Х +  2 Х 2 + …
2 Х 2 + …  Y =
Y =  0 +
0 +  1 Х 1* +
1 Х 1* +  2 Х 2* + …+
2 Х 2* + …+  m Хm +
m Хm + 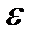 , (3.1)
, (3.1)
где Х 1* = Х; Х 2* = Х 2, …, Х m* = Х m.
Y =  0 +
0 +  1
1  +
+ 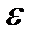
 Y =
Y =  0 +
0 +  1 Х * +
1 Х * + 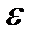 , (3.2)
, (3.2)
где Х * =  .
.
Оценка коэффициентов 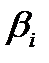 осуществляется по уравнению (3.1) с использованием метода МНК оценки для множественной линейной регрессии.
осуществляется по уравнению (3.1) с использованием метода МНК оценки для множественной линейной регрессии.
Выражение (3.2) соответствует парной линейной регрессии.
Нелинейности второго вида приводятся к линейным с помощью операции логарифмирования.
Пример.
В качестве примера рассмотрим производственную функцию Кобба-Дугласа
Y = A 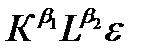 , (3.3)
, (3.3)
где Y – объем производства; К – затраты капитала; L – затраты труда; 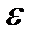 - случайное возмущение;
- случайное возмущение;  1,
1,  2 – коэффициенты частной эластичности объема производства Y по затратам капитала К и труда L; A – постоянный коэффициент.
2 – коэффициенты частной эластичности объема производства Y по затратам капитала К и труда L; A – постоянный коэффициент.
Логарифмируя обе части уравнения (3.3) для i – го наблюдения, получим
ln yi = ln A + 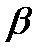 1 ln Ki +
1 ln Ki + 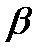 2 ln Li + ln
2 ln Li + ln 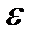 i . (3.4)
i . (3.4)
Переобозначив переменные в (3.4)
yi * = ln yi ; Х 1 i = ln Ki ; Х 2 i = ln Li ;  0 = ln A;
0 = ln A;  = ln
= ln 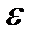 i,
i,
получим
yi * =  0 +
0 +  1 Х 1 i +
1 Х 1 i +  2 Х 2 i +
2 Х 2 i +  (3.5)
(3.5)
Для выборки объема n в матричной форме уравнение (3.5) запишется в виде
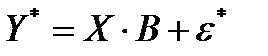 , (3.6)
, (3.6)
где  = (y1 * , y2 * ,…, yn * ) T ; В = (
= (y1 * , y2 * ,…, yn * ) T ; В = ( 0,
0,  1 ,
1 ,  2 ) Т ;
2 ) Т ;

 .
.
Таким образом, алгоритм оценки параметров нелинейной регрессии состоит из предварительного преобразования нелинейной модели к линейной и оценки ее параметров обычным образом с использованием МНК. После чего осуществляются обратные преобразования и возврат к исходному нелинейному уравнению.
Для нелинейной регрессии значимость уравнения в целом характеризуется также, как и в линейной регрессии с помощью коэффициента детерминации  :
:
 = 1 – (1 – R 2)
= 1 – (1 – R 2)  , (3.7)
, (3.7)
где R 2 = 1 - 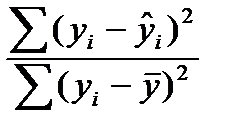 . (3.8)
. (3.8)
В (3.8)  определяется по исходному нелинейному уравнению регрессии.
определяется по исходному нелинейному уравнению регрессии.
Примечание. Значимость коэффициентов регрессии осуществляется по линеаризованному уравнению. Поэтому, если в линеаризованном уравнении присутствует не bi, а ln bi, тогда Т -статистика этого параметра будет:
Тbi =  ,
,
и характеризует значимость не самого коэффициента bi, а его логарифма.
При описании статистической зависимости между экономическими переменными различными функциональными соотношениями выбор наилучшей модели осуществляется следующим образом. Выбираются уравнения с наибольшими значениями  . Если таких уравнений несколько (примерно с одинаковыми значениями
. Если таких уравнений несколько (примерно с одинаковыми значениями  ), то выбирается модель, у которой наименьшая
), то выбирается модель, у которой наименьшая  или наименьшая остаточная дисперсия
или наименьшая остаточная дисперсия
 .
.






