Для проверки статистической значимости коэффициентов регрессии используется случайная величина

Т _bi = b_i / S_bi, i = 0, 1, 2, …, m, (2.12)

имеющая распределение Стьюдента.

Правило проверки заключается в выполнении следующих действий.

1. Вычисляется наблюдаемое значение критерия для i -го коэффициента (2.12).

2. По заданным уровням значимости 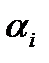, i = 0, 1, …, m и степени свободы по таблице распределения Стьюдента определяются критические значения распределения t _крит().

3. Сравниваются наблюдаемые и критические значения между собой. Результатом сравнения является вывод о значимости коэффициентов b ₀, b ₁, b ₂, …, b_m.

 

2. Интервальные оценки коэффициентов уравнения регрессии.

Так как объем выборки ограничен, то b ₀, b ₁, b ₂, …, b _m – случайные величины, поэтому желательно найти доверительные интервалы для истинных значений ₀, ₁, ₂, …, _m. Для этого также используется t – критерий Стьюдента. Интервальные оценки коэффициентов уравнения регрессии определяются по формулам

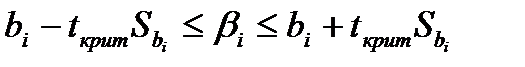(2.13)

3. Проверка общего качества уравнения регрессии.

Для этой цели, как и в случае парной регрессии, используется коэффициент детерминации R²:

R ² = 1 - е_i ² / (y_i - 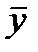)². (2.14)

 

В множественной регрессии каждая новая переменная х_i приводит к увеличению R ², хотя это еще не означает, что уравнение регрессии становится более значимым. Чтобы исключить эту зависимость от числа переменных, иногда используют так называемый скорректированный коэффициент детерминации:

 

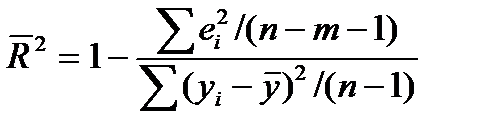. (2.15)

Или эту формулу можно преобразовать к виду:

 

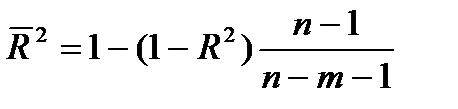. (2.16)

 

4. Анализ статистической значимости коэффициента детерминации.

По величине R ² можно только предполагать насколько значимо или не значимо уравнение регрессии. Даже при небольшой величине R ² (< 0,5) не всегда следует отказываться от уравнения регрессии. Для этого необходимо проверить статистическую значимость самого коэффициента детерминации. Для чего проверяются гипотезы

Н ₀: R ² = 0,

Н ₁: R ² > 0.

 

Для проверки используется распределение Фишера. Вычисляется F – статистика:

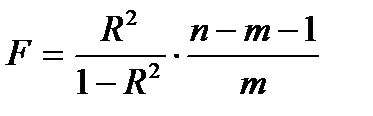. (2.17)

 

При заданном уровне значимости по таблице критических точек Фишера находится f_кр, и если F > f_кр, то R ² статистически значим.

 

5. Проверка выполнимости предпосылок МНК с помощью статистики Дар бина-Уотсона.

Статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации R ² еще не гарантируют высокое качество уравнения регрессии. Если не выполняются необходимые предпосылки МНК об отклонениях , то коэффициенты регрессии и само уравнение являются не вполне состоятельными, а это значит что внешние признаки «хорошего» уравнения не отвечают действительности. Поэтому следующим этапом проверки качества уравнения регрессии является проверка соответствия выборочных данных предпосылкам МНК. Для этого воспользуемся статистикой Дарбина – Уотсона, которая устанавливает, в частности, наличие или отсутствие статистической зависимости между ошибками . Так как истинные значения неизвестны, то проверка осуществляется в отношении оценок ошибок е_i. При этом проверяется некоррелированность соседних значений е_i.

Статистика Дарбина – Уотсона DW рассчитывается по формуле:

 

. (2.18)

 

 

По таблицам критических точек Дарбина – Уотсона, входными параметрами которых являются: n – число наблюдений; m – количество объясняющих переменных; - уровень значимости, определяются два числа: d ₁ – нижняя граница; d_u – верхняя граница.

Выводы осуществляются по следующей схеме.

Если DW < d ₁, то это свидетельствует о положительной автокорреляции остатков.

Если DW > 4 - d ₁, то это свидетельствует об отрицательной автокорреляции остатков.

При d_u < DW < 4 – d_u принимается гипотеза об отсутствии автокорреляции остатков.

Если d ₁ < DW < d_u или 4 – d_u < DW < 4 – d ₁, то остается неопределенность по вопросу наличия или отсутствия автокорреляции остатков.

В случае обнаружения признака автокорреляции необходимо скорректировать уравнение регрессии в соответствии с рекомендациями Главы IV

 

 

6. Прогноз значений зависимой переменной.

По аналогии с парной регрессией может быть построена интервальная оценка для среднего значения прогноза. Здесь речь идет о возможных значениях Y_р при определенных значениях вектора объясняющей переменной Х_р = (1, х _{1 р} , х _{2 р} , …, х_mр)^т.

Интервальный прогноз для среднего значения вычисляется следующим образом:

_р t_кр S 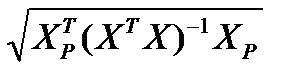, (2.19)

 

где _р = b ₀ + b ₁ x _{1 р} + b ₂ x _{2 р} + …+ b_m x_mр; t _кр – критическое значение, полученное по распределению Стьюдента при количестве степеней свободы 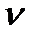= n - m- 1 и заданной вероятности /2.