На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Обозначим через Х 1, Х 2,…, Х m объясняющие переменные, влияющие на одну зависимую переменную Y. В этом случае возникает задача установления формы зависимости между переменными и определения функции регрессии. Тогда вместо парной регрессии рассматривается множественная регрессия.
Множественная регрессия – уравнение связи с несколькими объясняющими (независимыми) переменными:
Y = f (х 1, х 2, …, х m), (2.1)
т.е. условное математическое ожидание имеет вид (2.1):
М (Y / х 1, х 2, …, х m) = f (х 1, х 2, …, х m). (2.2)
Если между переменными наблюдается линейная зависимость, тогда модель множественной линейной регрессии можно представить в виде:
Y = 
0 + 1 Х 1 + 2 Х 2 + …+ m Х m +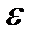 
, (2.3)
или для индивидуальных наблюдений i, i = 1,2,…, n:
yi = 0 + 1 xi 1 + 2 xi 2 + …+ m xi m + 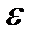i, (2.4)
= ( 0, 1, 2, …, m)т – вектор параметров, подлежащий определению.
Как и в случае парной регрессии по выборочным данным мы можем получить только эмпирическое уравнение модели:
Y = b 0 + b 1 Х 1 + b 2 Х 2 + …+ bm Хm + e. (2.5)
Или для индивидуальных наблюдений:
уi = b 0 + b 1 xi 1 + b 2 xi 2 + …+ bm xim + ei. (2.5)
Здесь В = (b 0, b 1, b 2, …, b m)т - оценка вектора .
Для определения оценок b 0, b 1, b 2, …, b m воспользуемся матричным МНК. Представим данные наблюдений и коэффициенты в матричном виде:
, 
, 
, 
.
Тогда уравнение множественной линейной регрессии второго рода запишем в виде: 
= Х В. (2.6)
Остаточная сумма квадратов в данном случае равна
. (2.7)
Результатом минимизации (2.7) является вектор:
B = (XT X)-1 XT Y. (2.8)
Оценки вектора В (2.8) являются несмещенными и эффективными, если выполняются предпосылки множественного регрессионного анализа [1].
Вычислим дисперсии коэффициентов регрессии b 0, b 1, b 2, …, b m, которые используются для оценки их точности, определения доверительных интервалов для теоретических коэффициентов 0, 1, 2, …, m и проверки соответствующих гипотез. Вариации оценок параметров будут определять и точность уравнения множественной регрессии. Для измерения их в многомерном регрессионном анализе используют ковариационную матрицу вектора оценок
.
Дисперсии коэффициентов вычисляются по формулам [1]:
, (2.9)
В (2.9) S 2 – дисперсия регрессии, вычисляется по формуле:
S 2 = (
(еi 2))/(n – m – 1), (2.10)
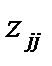- j -й (j = 0, 1,…, m) диагональный элемент матрицы
Z -1 = (XT X)-1. (2.11)
Оценка качества уравнения множественной линейной регрессии 2-го рода определяется следующими характеристиками:
- доверительными интервалами для коэффициентов регрессии и их статистической значимостью;
- оценкой коэффициента детерминации и его статистической значимостью;
- выполнением предпосылок МНК;
- прогнозом значений зависимой переменной и его параметрами
1. Проверка статистической значимости коэффициентов регрессии.
