При оценке параметров уравнения регрессии II – го рода предполагалось, что выполняются все предпосылки МНК, наиболее значимыми из которых являются:
1) Гомоскедастичность: 
для любых наблюдений 
и 
.
2) Отсутствие автокорреляции остатков: 
.
3) Отсутствие мультиколлинеарности: отсутствие сильной корреляционной зависимости между объясняющими переменными.
Однако эмпирические данные не всегда обладают такими характеристиками, в результате которых условия Гаусса-Маркова нарушаются, что в свою очередь приводит к оценкам модели с «плохими» статистическими свойствами (не состоятельные, не эффективные, смещенные).
Для «смягчения» нежелательных эффектов при построении регрессионных уравнений, повышения адекватности моделей существует ряд специальных методов корректировки моделей.
4.1.1. Гетероскедастичность
Явление, когда условия гомоскедастичности не соблюдаются, называется гетероскедастичностью, т.е. 
.
Методы обнаружения гетероскедастичности:
1) Графический.
Для скалярных (одномерных) моделей осуществляется графический анализ зависимости 
. Для множественной регрессии такие зависимости строятся для каждой объясняющей переменной 
отдельно или по оси абсцисс откладывают значения 
. Наличие гетероскедастичности проявляется в виде тенденции изменения распределения 
. Однако в связи со случайным характером объясняемой переменной по одной конкретной реализации судить о гетероскедастичности можно только предварительно. Наиболее объективно наличие гетероскедастичности можно подтвердить с помощью специальных тестов.
2) Тест ранговой корреляции Спирмена.
Тест ранговой корреляции Спирмена используется, когда есть предположение, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значений фактора Х. Этот тест заключается в проверке коррелированности абсолютных значений остатков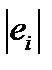 
и значений 
, т.е. проверяется не просто зависимость между ними, а ее приближение к линейной.
Коэффициент ранговой корреляции Спирмена вычисляется по формуле:
, (4.1)
где 
- число наблюдений; 
- разность между рангами 
.
Доказано, что если коэффициент корреляции 
(для генеральной совокупности) равен нулю, то статистика
(4.2)
имеет распределение Стьюдента с числом степеней свободы 
.
Если 
, то гипотеза =0 отклоняется в пользу гипотезы 
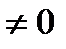, т.е. гетероскедастичность присутствует.
Для множественной регрессии такая проверка осуществляется для каждой объясняющей переменной.
3) Тест Голдфелда-Квандта.
При применении данного теста делается предположение, что дисперсия остатков возрастает пропорционально квадрату переменной 
. Этот тест в принципе дополняет тест Спирмена, так как здесь также предполагается, что отклонение 
пропорционально .
Смысл теста:
Шаг 1. Упорядочение 
переменных Х по возрастанию.
Шаг 2. Разделение совокупности Х на две группы с малыми и большими значениями, исключая из рассмотрения С - центральных наблюдений (С должно быть примерно равно четверти общего количества наблюдений). По каждой из этих выборок, объемами 
, строятся уравнения парной регрессии, из которых определяются остаточные суммы квадратов:
; 
. (4.3)
Шаг 3. Определяется F-статистика
, (4.4)
значение которой сравнивается с критическим значением 
, где 
- число объясняющих переменных.
Если 
> 
, то гетероскедастичность имеет место.
Рекомендации: 1) При = 30 рекомендуется выбирать с = 8, при =60 - с = 16; 2) Формально тест работает и без исключения наблюдений (когда n мало), но, как показывает опыт, при этом его мощность уменьшается.
Тесты Спирмена и Голдфелда-Квандта позволяют лишь обнаружить наличие или отсутствие гетероскедастичности, но не позволяют оценить количественно зависимость дисперсии от значений объясняющей переменной. С этой целью могут быть использованы тесты Уайта, Парка, Глейзера.
4) Тест Уайта.
Содержательный смысл этого теста состоит в следующем. Если в модели присутствует гетероскедастичность, то очень часто это связано с тем, что дисперсии ошибок некоторым образом (возможно, довольно сложно) зависят от регрессоров, а гетероскедастичность должна как-то отражаться в остатках обычной регрессии исходной модели. Этот тест является предпочтительным для анализа множественной регрессии, когда зависимость остатков от факторов носит сложный характер.
Этот тест предполагает, что дисперсия ошибок регрессии представляет собой квадратичную функцию от значений объясняющих переменных, т.е. при наличии одного фактора:
е2 = с0 +с1Х +с2Х2, (4.5)
или при наличии m факторов:
(4.6)
Примечание. Для упрощения анализа, слагаемые с парными произведениями факторов, как правило, не используются.
С помощью МНК оцениваются параметры (4.5) или (4.6). С использованием распределения Стьюдента осуществляется оценка статистической значимости коэффициентов сi c целью исключения из (4.5), (4.6) незначимых слагаемых.
О наличии или отсутствии гетероскедастичности судят по величине F – критерия Фишера:
, (4.6)
где R2 – коэффициент детерминации. Если > 
, то гетероскедастичность присутствует и в качестве модели при вычислении дисперсии может быть использована зависимость вида (4.5) или (4.6).
5) Тест Парка.
Здесь предполагается, что дисперсия остатков связана со значениями факторов функцией:
. (4.7)
Оценим (4.7) по МНК, предварительно прологарифмировав его
, (4.8)
где 
; 
.
Проверяется статистическая значимость коэффициента с 1 с использованием t -статистики (Т набл = с 1/ S c1). Если коэффициент значим, то модель дисперсии может быть принята в виде (4.7). Для множественной регрессии зависимость вида (4.7) формируется для переменной Хj, которая наибольшим образом влияет на распределение 
.
6) Тест Глейзера.
Этот тест основан на проверке зависимостей остатков 
от объясняющих переменных вида:
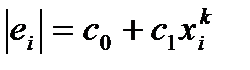(4.9)
Регрессии строятся при различных значениях k и выбирается та функция, для которой коэффициент с 1 наиболее значим статистически (проверяется с помощью критерия Стьюдента) или наиболее значимо уравнение (4.9) в целом (используется распределение Фишера для R 2). Обычно k =…; -1; -0,5; 0,5; 1;…
Методы смягчения проблемы гетероскедастичности.
Основным методом коррекции влияния гетероскедастичености является взвешенный метод наименьших квадратов (ВМНК).
Суть ВМНК: минимизируется не сумма квадратов остатков 
, а взвешенная сумма квадратов
, (4.10)
где 
- вес i -ой ошибки.
В случае гетеросекдастичности в качестве выбирается величина обратная дисперсии, с целью уменьшения веса измерений с большими ошибками:
. (4.11)
В этом случае ВМНК можно трансформировать в МНК, если принять, что уравнение регрессии имеет вид:
. (4.12)
С помощью замены переменных (4.12) приводится к стандартному уравнению регрессии и посредством процедуры МНК вычисляются оценки b 0 и b 1.
Для множественной регрессии оценка коэффициентов уравнения вычисляется с помощью ВМНК по формуле:
, (4.13)
где R -1 - диагональная матрица, элементами которой являются 
, 
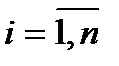, Здесь приняты обозначения аналогичные рассмотренным в Главе II.
Для реализации алгоритма ВМНК (в случае множественной регрессии) на ЭВМ с помощью комплексных функций ЛИНЕЙН и РЕГРЕССИЯ необходимо исходное уравнение преобразовать к виду:
, (4.14)
где 
, 
, 
, …
Эмпирическая корректировка уравнения регрессии.
Так как значения дисперсий 
на самом деле неизвестны, то в качестве их оценок предлагается использовать наиболее предпочтительное представление 
, полученное с помощью одного из выше рассмотренных тестов (Уайта, Парка, Глейзера). В этом случае аргументы уравнения (4.14) будут следующими:
, 
, 
, …, 
.
Пример. Пусть по выборке с помощью МНК было синтезировано уравнение регрессии:
. (4.15)
При этом получен ряд остатков е i. Применим к е i тест Уайта, т.е. оценим регрессию вида:
. (4.16)
С помощью обычного МНК находим с i. Для реализации ВМНК разделим все составляющие (4.15) на 
и оценим его. В результате чего будут получены скорректированные оценки 
и уравнение регрессии будет некоторым образом адаптировано к переменным дисперсиям ошибок измерений.
4.1.2. Автокорреляция.
Определение и основной критерий обнаружения автокорреляции – критерий Дарбина-Уотсона DW были рассмотрены ранее (Глава II). Здесь рассмотрим только основные методы корректировки явления автокорреляции.
1) Так как автокорреляция чаще всего вызывается спецификацией модели, то необходимо, прежде всего, скорректировать саму модель. Возможно, автокорреляция вызвана отсутствием в модели некоторой важной объясняющей переменной, либо неправильно выбрана структура или вид функциональной зависимости. В этом случае нужно ввести дополнительную переменную, либо скорректировать вид функциональной зависимости. Если вышеизложенные действия не позволили в полной мере решить проблему автокорреляции, то следует применить авторегрессионную схему.
2) Авторегрессионная схема первого порядка.
Предполагается, что случайные отклонения подвержены автокорреляции 1-го порядка, т.е.
, (4.17)
где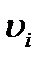 
(i = 1,…, n) представляет белый шум, т.е. последовательность независимых нормально распределенных случайных величин с нулевой средней и дисперсией 
; 
- параметр, называемый коэффициентом авторегрессии.
В этом случае исходное уравнение регрессии приводится к виду:
, (4.18)
где 
Значение коэффициента 
можно оценить с помощью коэффициента корреляции 
из известного соотношения критерия Дарбина-Уотсона:
DW =2(1- ),
т.е. 
. (4.19)
Существует еще ряд методов оценки коэффициента (метод Кохрана-Оркатта, метод Хилдрета-Лу и др.). На них останавливаться не будем.
4.1.3. Мультиколлинеарность.
Мультиколлинеарность – это явление связано с наличием линейной зависимости между факторами Х j регрессионной модели.
Одно из негативных последствий мультиколлинеарности заключается в том, что невозможно определить силу изолированного влияния факторов на объясняемую переменную.
При построении многофакторной модели (множественной регрессии) необходимо соблюдение следующего правила:
| Факторы, включаемые в модель, должны быть сильно связаны с зависимой переменной и не должны быть связаны между собой. |
Мультиколлинеарность присутствует во всех экономических моделях, где все переменные экономических объектов должны быть взаимосвязаны между собой. Иначе экономическая система не будет существовать.
Поэтому мультиколлинеарность была, есть и будет, бороться с ней бесполезно, но учитывать ее при построении множественных регрессионных моделей необходимо.
Методы обнаружения мультиколлинеарности.
Признаки наличия мультиколлинеарности:
1) Коэффициент детерминации R 2 достаточно высок, но все или некоторые коэффициенты уравнения регрессии статистически не значимы (низкие t -статистики);
2) Высокие парные коэффициенты корреляции.
Для проверки этого признака формируется определитель матрицы парных коэффициентов между объясняющими переменными:
R = 
, (4.20)
где 
. (4.21)
Матрица R – симметричная, причем на главной диагонали стоят единицы, т.е. 
=1. При полном отсутствии корреляции между факторами 
=0, при 
, и определитель R равен 1. Если же между факторами существует полная линейная зависимость, т.е. =1, то det R = 0.
Таким образом, чем ближе к нулю detR, тем сильнее мультиколлинеарность. Вывод о наличии мультиколлинеарности делается по результатам проверки нулевой гипотезы Н 0: det R = 1, при альтернативной гипотезе Н 1: det R = 0.
Статистическая проверка гипотез:
Н 0: det R = 1;
Н 1: det R = 0
осуществляется с помощью 
- распределения.
Величина
(4.22)
сравнивается с критическим значением 
(
), где n – объем выборки, m – количество объясняющих переменных.
Если 
> , то Н0 отклоняется и делается вывод о наличии мультиколлинеарности.
3) Высокие частные коэффициенты корреляции.
Частные коэффициенты корреляции – это коэффициенты корреляции между двумя факторами, «очищенные» от влияния других факторов. Например для трех факторов Х 1, Х 2, Х 3 частный коэффициент корреляции для Х 1, Х 2 будет:
, (4.23)
где 
- парный коэффициент корреляции между Х 1 и Х 2;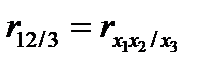 
- частный коэффициент корреляции между Х 1 и Х 2.
Схема вычисления элементов матрицы частных коэффициентов корреляции:
а) Обращение матрицы парных коэффициентов корреляции (4.20)
R -1 = C = 
; (4.24)
б) Вычисление частных коэффициентов корреляции
. (4.24)
Частные коэффициенты корреляции могут быть использованы для определения «чистого» влияния Хj на Y и ранжирования таким образом зависимости Хj на результат. Для этого составляется расширенная матрица частных коэффициентов:
| Y | X1 | X2 | … | Xm | |
| Y | 
| 
| … | 
| |
| X1 | 
| 
| … | 
| |
| X2 | 
| 
| … | 
| |
| … | … | … | … | … | … |
| Xm | 
| 
| 
| … |
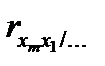
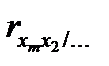
Частные коэффициенты корреляции 
определяют степень линейной зависимости Хj и Y.
Методы устранения мультиколлинеарности.
Мультиколлинеарность можно и не корректировать, если целью задачи является прогноз будущих значений зависимой переменной. Если же целью исследования является определение степени влияния каждой из объясняющих переменных на Y, то мультиколлинеарность исказит истинные связи между переменными. В этом случае мультиколлинеарность необходимо устранить. Единого метода устранения мультиколлинеарности не существует, однако одним из возможных методов является исключение из модели переменных.
Суть метода в следующем:
1. Определяется расширенная матрица частных коэффициентов корреляции. Осуществляется ранжирование переменных Хj в соответствие с коэффициентами .
2. В модели оставляют наиболее значимые аргументы, т.е. с большими значениями , но при этом, чтобы 
были бы низкими.
