До появления ЭВМ (компьютеров) всюду при вычислениях использовалась десятичная система счисления. Интерес к другим системам носил либо исторический, либо познавательный характер. С появлением ЭВМ возникла задача сделать их устройство как можно более компактным и эффективным. Это привело к тщательному изучению систем счисления с целью нахождения наиболее подходящей из них. Предпочтение было отдано двоичной системе счисления. Для радиоэлектронных элементов, которые, в основном, используются в вычислительных машинах, характерно наличие двух устойчивых состояний. Например, электронная лампа может пропускать ток или не пропускать. По тому же принципу «да» или «нет» работают и полупроводниковые элементы, которые широко применяются в вычислительной технике. Эти свойства радиоэлектронных элементов и служат основной причиной того, что именно двоичная система оказалась наиболее удобной для вычислительных машин. Другое преимущество двоичной системы состоит в простоте выполнения арифметических действий.
С точки зрения принципа работы любая ЭВМ может рассматриваться как состоящая их трех основных частей:
1) арифметического устройства, предназначенного для выполнения операций над числами;
2) запоминающего устройства, предназначенного для приема, хранения и выдачи чисел;
3) устройства управления, предназначенного для управления автоматической работой машины.
Основным арифметическим действием, выполняемым в машине, является сложение, т.к. в двоичной системе счисления вычитание заменяется сложением с противоположным числом, деление выполняется путем последовательного вычитания, умножение сводится к сдвигам множимого и нескольким сложениям. Поэтому основным элементом арифметического устройства является многоразрядный двоичный сумматор, осуществляющий сложение двух двоичных чисел.
Многоразрядный сумматор представляет собой последовательное соединение одноразрядных сумматоров, каждый из которых осуществляет сложение цифр одного разряда и перенос в старший разряд.
Двоичный одноразрядный сумматор должен иметь три входа. На двух из них поступают значения соответствующих слагаемых, а третий вход для возможного переноса из младшего разряда. Выхода два. Один для суммы, другой – для возможного переноса в старший разряд.
Работа двоичного сумматора может быть описана с помощью таблицы, в которой через А и В обозначены входы, на которые подаются цифры соответствующего разряда слагаемых, S – выход, содержащий цифру данного разряда в сумме, а через Z l и Z 2 – переносы соответственно из младшего разряда в данный и из данного в старший.
|
| А | B | Z 1 | S | Z 2 |
Возникает вопрос: «Зачем учителю начальных классов знания о позиционных системах, отличных от десятичной?»
1. В разное время у разных народов применялись системы счета, отличные от десятичной, т.е. интерес представляет история возникновения десятичной системы счисления.
2. В настоящее время получили большое распространение ЭВМ. Большинство таких машин «считает» в двоичной системе счисления.
3. Изучая другие системы счисления, можно лучше понять сущность десятичной системы счисления.
Вопросы и задания для самопроверки
1. В чем суть позиционной системы счисления?
Как записывается натуральное число в системе счисления с основанием р?
2. Запишите десятичные числа 125 и 136 в двоичной, троичной, пятеричной, двенадцатиричной системах счисления.
3. Сформулируйте алгоритмы сложения, вычитания, умножения и деления для чисел, записанных в десятичной системе счисления.
4. Выполните действия над числами, записанными в восьмеричной системе счисления.
а) 4312 + 2357; в) 721 × 34;
б) 6614 – 3506; г) 5220: 76.
ОГЛАВЛЕНИЕ
| Предисловие.......................................................................................... | |
| ГЛАВА I. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ | |
| § 1. Множество и его элементы........................................................ | |
| § 2. Способы задания множеств...................................................... | |
| § 3. Числовые множества................................................................... | |
| § 4. Отношения между множествами.............................................. | |
| § 5. Множество всех подмножеств данного множества. Универсальное множество................................................................ | |
| § 6. Пересечение множеств................................................................ | |
| § 7. Объединение множеств............................................................... | |
| § 8. Свойства, связывающие операции пересечения и объединения....................................................................................... | |
| § 9. Вычитание множеств. Дополнение множества................... | |
| § 10. Свойства вычитания и дополнения...................................... | |
| § 11. Декартово умножение множеств........................................... | |
| § 12. Разбиение множества на классы........................................... | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА II. СООТВЕТСТВИЯ, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ | |
| § 1. Соответствия между элементами множеств......................... | |
| § 2. Граф соответствия....................................................................... | |
| § 3. Взаимно однозначные соответствия...................................... | |
| § 4. Обратное соответствие. Противоположное соответствие........ | |
| § 5. Отношения. Их графы и графики............................................. | |
| § 6. Свойства отношений................................................................... | |
| § 7. Отношение эквивалентности. Связь между отношением эквивалентности и разбиением множества на классы.............. | |
| § 8. Примеры отношений эквивалентности.................................. | |
| § 9. Отношение строгого порядка................................................... | |
| § 10. Отношение нестрогого порядка............................................. | |
| § 11. Упорядоченные множества..................................................... | |
| § 12. Отображение множества в множество................................. | |
| § 13. Виды отображений. Обратное отображение..................... | |
| § 14. Эквивалентные множества...................................................... | |
| § 15. Мощность множества. Счетные множества....................... | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА III. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ | |
| § 1. Правило суммы. Правило произведения............................... | |
| § 2. Виды комбинаторных задач и способы их решения......... | |
§ 3. Свойства чисел 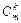 ..................................................................... .....................................................................
| |
| § 4. Примеры решения комбинаторных задач............................. | |
| § 5. Перестановки и сочетания с повторениями.......................... | |
| § 6. Первоначальные понятия теории вероятностей................. | |
| § 7. Случайные события.................................................................... | |
| § 8. Формула для непосредственного подсчета вероятности. | |
| § 9. Применение формул числа перестановок и сочетаний к вычислению вероятностей..................................... | |
| § 10. Относительная частота. Статистическое определение вероятности.................................................................. | |
| § 11. Операции над событиями........................................................ | |
| § 12. Теорема о вероятности суммы несовместных событий.. | |
| § 13. Условная вероятность.............................................................. | |
| § 14. Теоремы о вероятности произведения двух событий...... | |
| § 15. Теорема о вероятности суммы двух совместных событий................................................................................................... | |
| § 16. Формула полной вероятности. Формула Байеса............. | |
| § 17. Формула Бернулли.................................................................... | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА IV. МАТЕМАТИЧЕСКИЕ УТВЕРЖДЕНИЯ И ИХ СТРУКТУРА | |
| § 1. Понятие. Содержание и объем понятия................................. | |
| § 2. Родо-видовые и другие отношения понятий......................... | |
| § 3. Определение понятий.................................................................. | |
| § 4. Требования, предъявляемые к определению понятий....... | |
| § 5. Высказывания. Элементарные и составные высказывания........................................................................................ | |
| § 6. Конъюнкция высказываний....................................................... | |
| § 7. Дизъюнкция высказываний....................................................... | |
| § 8. Отрицание высказываний.......................................................... | |
| § 9. Импликация высказываний....................................................... | |
| § 10. Эквиваленция высказываний. Тавтология.......................... | |
| § 11. Одноместные предикаты......................................................... | |
| § 12. Многоместные предикаты....................................................... | |
| § 13. Кванторы...................................................................................... | |
| § 14. Операции над предикатами.................................................... | |
| § 15. Строение теоремы..................................................................... | |
| § 16. Теорема, обратная данной. Необходимое и достаточное условие........................................................................ | |
| § 17. Теорема, противоположная данной..................................... | |
| § 18. Математические доказательства.......................................... | |
| § 19. Правильные умозаключения.................................................. | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА V. АЛГОРИТМЫ И ИХ СВОЙСТВА | |
| § 1. Определение алгоритма............................................................. | |
| § 2. Формальное исполнение алгоритма....................................... | |
| § 3. Алгоритмический язык................................................................ | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА VI. АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ МНОЖЕСТВА ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ | |
| § 1. Понятие об аксиоматическом методе построения теории........ | |
| § 2. Аксиомы Пеано. Аксиоматическое определение целых неотрицательных чисел........................................................ | |
| § 3. Метод математической индукции........................................... | |
| § 4. Сложение целых неотрицательных чисел............................ | |
| § 5. Основные свойства сложения целых неотрицательных чисел | |
| § 6. Умножение целых неотрицательных чисел......................... | |
| § 7. Основные свойства умножения целых неотрицательных чисел.................................................................... | |
| § 8. Сравнение целых неотрицательных чисел........................... | |
| § 9. Вычитание целых неотрицательных чисел. Основные свойства вычитания........................................................ | |
| § 10. Деление целых неотрицательных чисел............................. | |
| § 11. Правила деления........................................................................ | |
| § 12. Деление с остатком................................................................... | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА VII. ТЕОРЕТИКО-МНОЖЕСТВЕННЫЙ ПОДХОД К ПОСТРОЕНИЮ МНОЖЕСТВА ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (КОЛИЧЕСТВЕННАЯ ТЕОРИЯ) | |
| § 1. Понятие целого неотрицательного числа............................. | |
| § 2. Сравнение целых неотрицательных чисел........................... | |
| § 3. Сложение целых неотрицательных чисел............................ | |
| § 4. Вычитание целых неотрицательных чисел.......................... | |
| § 5. Теоретико-множественное истолкование умножения....... | |
| § 6. Теоретико-множественное истолкование деления и деления с остатком........................................................................... | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА VIII. НАТУРАЛЬНОЕ ЧИСЛО КАК РЕЗУЛЬТАТ ИЗМЕРЕНИЯ ВЕЛИЧИН | |
| § 1. Понятие числа............................................................................... | |
| § 2. Действия над натуральными числами – мерами величин | |
| § 3. Общая схема решения задач, связанных с обоснованием выбора действий и наглядной иллюстрацией условия задачи.............................................................................................. | |
| Вопросы и задания для самопроверки...................................... | |
| ГЛАВА IX. СИСТЕМЫ СЧИСЛЕНИЯ | |
| § 1. Непозиционные системы счисления....................................... | |
| § 2. Позиционные системы счисления............................................ | |
| § 3. Перевод целых неотрицательных чисел из одной позиционной системы счисления в другую................ | |
| § 4. Восьмеричная система счисления........................................... | |
| § 5. Двоичная система счисления.................................................... | |
| § 6. Другие позиционные системы счисления.............................. | |
| § 7. Компьютеры и системы счисления......................................... | |
| Вопросы и задания для самопроверки...................................... |
[1] Леонард Эйлер (1707-1783) – российский математик,
Джон Венн (1834-1923) – английский ученый.
[2] Август де Морган (1806-1871) – английский логик.
[3] Блэз Паскаль (1623-1662) – французский математик
[4] Томас Байес (1702-1761) – английский математик
[5] Даниил Бернулли (1700-1782) – швейцарский математик
[6] Джузеппе Пеано (1858-1932) – итальянский математик и логик






