Действия над натуральными числами – мерами величин

В нижеследующих определениях будем считать, что числа
p, q Î N, а, в, с – отрезки, е – единичный отрезок.

Определение суммы натуральных чисел.

р + q = m_е (а), если а = в + с, m_е (в) = р, m_е (с) = q.

Таким образом, сумму двух натуральных чисел определяют через длину суммы отрезков в и с (рис. 1).

 

 

Рис. 1

Аналогия с теоретико-множественным подходом представлена на рис 2.

р + q = n (В С), если В С = Æ. n (В) = р. n (С) = q.

B C

р _эл. q _эл.

 

Рис. 2

Замечание. Здесь и далее в этом параграфе «эл» – это сокращение слова «элементов».

Определение разности натуральных чисел.

р – q = m_е (с), если а = в + с, m_е (а) = р, m_е (в) = q.

Таким образом, разность двух натуральных чисел определяют через длину «разности» двух отрезков а и в.

p – q = n (A\B),если В Í А, n (A) = p, n (B)= q.

Аналогия с теоретико-множественным подходом представлена на рис. 3.

А

р_эл.

А \ В

(? = эл)

Рис. 3

Определение произведени я натуральных чисел.

p · q = т_{е 1} (а), если т_{е 1} (е) = р, т_e (а) = q, е ₁ – новый единичный отрезок (рис. 4).

 

а

Рис. 4

Таким образом, умножение натуральных чисел отражает переход к новой (более мелкой) единице длины е ₁ по сравнению со старой единицей длины е.

Аналогия с теоретико-множественным подходом представлена на рис 5.

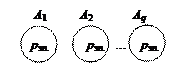p · q = n (A ₁ A ₂ ... A_q),

если A_i A_j =Æ (i ≠ j).

n (А ₁) = n (А ₂) =... = n (A_q) = p.

 

Рис. 5

Определение частного натуральных чисел.

1 случай. p: q = т_{е 1} (а), если т_е (а) = р, т_е (е ₁) = q; т_{е 1} (a) Î N, т.е. в отрезок а отрезок е ₁ укладывается целое число раз (рис. 6).

2 случай. р: q = т_е (е ₁), где т_е (а) = р, т_{е 1}(a) = q, m_e (е ₁) Î N (рис. 7).

a Рис. 6	a Рис. 7

Единичный отрезок е ₁ не задан, он получается в результате дробления отрезка а на q равных отрезков.

Таким образом, деление натуральных чисел связано с разбиением отрезка и отражает переход к новой (более крупной) единице длины е ₁, по сравнению со старой единицей длины е.

Аналогия с теоретико-множественным подходом представлена на рисунках 8, 9.

1 случай. Множество А, в котором р элементов, разбито на q равночисленных подмножеств А ₁, А ₂,..., А_q, в каждом из которых по q элементов.

Тогда р: q = n, где n – число подмножеств разбиения. Т.е. 1 случай – это задача на нахождение числа подмножеств разбиения.

 

 

Рис. 8

2 случай. Множество А, в котором р элементов, разбито на q равночисленных подмножеств А ₁, А ₂,..., А_q. Тогда р: q = n, где n – число элементов в каждом из подмножеств разбиения.

Т.е. 2 случай – это задача на нахождение числа элементов в подмножествах разбиения.

 

 

Замечание 1. Так как сумма, разность, произведение, частное определяются через меры соответствующих отрезков p + q = т_e (а), р · q = т_{е 1} (а) и т.д., то владея этими операциями (т.е. зная таблицы сложения и умножения) можно, в свою очередь, находить меры длин отрезков:

т_e (а)= р + q; m_e (с) = р – q; т_{е 1}(a) = p · q; т_{е 1} (a) = р: q.

Замечание 2. Так как законы арифметических действий являются общими для результатов измерения различных величин, то численный результат задач не зависит от наименования величины. Это позволяет, для простоты рассуждения, заменить задачу, связанную с какой-то величиной, на сходную задачу, связанную с длиной, решив которую, можно получить численный ответ исходной задачи.