Пусть в результате испытания могут появиться n событий, независимых в совокупности. Вероятности появления каждого события известны. Как найти вероятность того, что произойдет хотя бы одно из этих событий (т.е. или одно, или два, …, или все n событий)?
J V Заранее известны вероятности прихода на лекцию каждого студента группы СУА. Какова вероятность того, что на лекции будет хотя бы один студент этой группы?
Теорема. Вероятность появления хотя бы одного из событий А1,…, Аn, независимых в совокупности, равняется:
, где 
- противоположные события.
Доказательство:
Событие А – появление хотя бы одного из событий. Тогда Ā – непоявление ни одного события (не наступит ни 1-е, ни 2-е, …, ни n-е событие).
Ā = Ā1 Ā2 … Ān
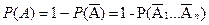
Т.к. события независимы 
и
<
V Пусть события 
значат соответственно, что группы ГКСР, СУА, ЗИОД пришли на лекцию в полном составе. Будем считать эти события независимыми и пусть 
(J либо пришли, либо нет). Найти вероятность того, что на лекции есть хотя бы одна группа в полном составе.
Ï Событие А – «хотя бы одна группа пришла в полном составе».
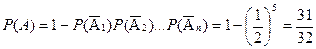N
