Мы перебрали все варианты. Других просто не может быть. Обратим внимание: любая сумма событий даст нам уже описанное событие (в исходах)
{w1, w2} + {w3} = {w1, w2, w3}
Любое произведение так же уже есть
{w1, w2} * {w2, w3} = {w2}
Таким образом, мы получили набор подмножеств (событий), обладающий определенными свойствами.
σ – алгеброй называют непустую систему подмножеств F некоторого множества Ω, удовлетворяющую следующим условиям:
- Если подмножество А Ì F, то Ā Ì F.
- Если А1,…, Аn,… Ì F
то А1ÈА2È…ÈАnÈ…Ì F и
А1ÇА2Ç…ÇАnÇ…Ì F.
Очевидно, что ÆÌ F и Ω Ì F. В примере с пирамидой система событий (подмножеств) образует σ – алгебру.
{w1}, {w2}, {w3},{w4},
{w1, w2}, {w2, w3}, {w1, w3},{w2, w4},{w1, w4},{w3, w4},
{w1, w2, w3}, {w1, w2, w4}, {w2, w3, w4}, {w1, w3, w4},
{w1, w2, w3, w4}, Æ.
При аксиоматическом определении вероятности у нас имеется множество W - пространство неравновозможных элементарных исходов 
. События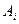 
являются подмножествами W и образуют σ–алгебру. Пусть каждому событию А поставлено в соответствие число Р(А).
Числовую функцию Р(А) называют вероятностью, если она удовлетворяет следующим аксиомам:
Аксиома 1.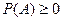 
.
Аксиома 2.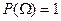 
.
Аксиома 3. Для попарно несовместных событий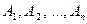 
справедливо равенство 
.
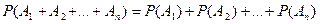Тройку <Ω, F, P>, где W - пространство элементарных исходов, F - σ – алгебра событий, Р - вероятность, называют вероятностным пространством.
V Простейшее вероятностное пространство – при бросании монетки (орел, решка)
Ï Ω = {w0, wp}
A1 A2 Ω
F = {Æ, {w0}, {wp}, {w0, wp}}
P(A1) = P(A2) = ½, Р(Æ)=0, Р(Ω)=1. N
