Минором Мij элемента aij определителя D =  , где i и j меняются от 1 до п, называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.
, где i и j меняются от 1 до п, называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.
Например, минор М12, соответствующий элементу а12 определителя
D = 
получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.
М12 = 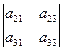 .
.
3. Вычислить все миноры определителя D =  .
Р е ш е н и е. М11 = .
Р е ш е н и е. М11 =  ; М12 = ; М12 =  ;
М13 = ;
М13 =  ; М21 = ; М21 =  ; М22 = ; М22 =  ;
М23 = ;
М23 =  ; М31 = ; М31 =  М32 = М32 =  ;
М33 = ;
М33 = 
|
Алгебраическим дополнением элемента aij определителя называется минор М ij этого элемента, взятый со знаком (- 1) i +j. Алгебраическое дополнение элемента aij принято обозначать А ij. Таким образом, Аij = (- 1) i + j M ij.
4. Найти алгебраические дополнения элементов а13, а21, а31 определителя
D =  .
Р е ш е н и е.
А13 = (- 1)1+3 .
Р е ш е н и е.
А13 = (- 1)1+3  А21 = (- 1)2+1
А21 = (- 1)2+1  А31 = (- 1)3+1
А31 = (- 1)3+1 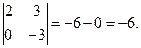
|






