Если число строк матрицы не равно числу столбцов (m ≠ n), то матрица называется прямоугольной. Таковы, например, матрицы
А =  , В =
, В =  .
.
Если число строк равно числу столбцов (m = n), то матрица называется квадратной. Например, квадратными являются матрицы
А =  , В =
, В =  .
.
Число строк или столбцов квадратной матрицы называется ее порядком. Так, в последнем примере порядок матрицы А равен 2, а порядок матрицы В равен 4.
Рассмотрим квадратную матрицу порядка п:
А =  .
.
Диагональ, содержащую элементы а11, а22, …, апп, будем называть главной, а диагональ, содержащую элементы а1п, а2,п-1, …, ап1, - побочной (или вспомогательной).
Среди квадратных матриц выделим матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали:
А =  .
.
Такие матрицы называются диагональными; например, матрицы
А =  , В =
, В = 
являются диагональными матрицами второго и четвертого порядка.
Если у диагональной матрицы все числа главной диагонали равны между собой, т.е. а11 = а22 = … = апп, то такая диагональная матрица называется скалярной. Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной и обозначается буквой Е:
Е =  .
.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается так:
О = 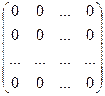 .
.
В прямоугольной матрице типа т×п возможен случай, когда т = 1. При этом получается матрица-строка:
А = (а11 а12 … а1п).
В случае, когда п = 1, получаем матрицу-столбец:
В =  .
.
Такие матрицы- строки и матрицы-столбцы иначе будем называть векторами.




