Пусть дана система уравнений

Рассмотрим матрицу, составленную из коэффициентов при неизвестных:
А = 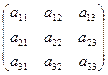 .
.
Свободные члены и неизвестные можно записать в виде матриц-столбцов:
В = 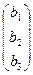 , X =
, X =  .
.
Тогда, используя правило умножения матриц, эту систему уравнений можно записать так:
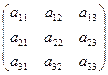
 =
= 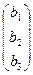 или АХ = В.
или АХ = В.
Это равенство называется простейшим матричным уравнением.
Такое уравнение решается следующим образом. Пусть матрица А — невырожденная (D ≠ 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем
А-1(АХ) = А-1В.
Используя сочетательный закон умножения, перепишем это равенство в виде
(А-1А)Х = А-1В.
Поскольку А-1А = Е и ЕХ = Х, находим
Х = А-1В.
Таким образом, чтобы решить матричное уравнение, нужно:
1°. Найти обратную матрицу А-1.
2°. Найти произведение обратной матрицы А-1 на матрицу-столбец свободных членов В, т. е. А-1В.
3°. Пользуясь определением равных матриц, записать ответ.
1. Решить матричное уравнение  Р е ш е н и е. 10. Будем искать обратную матрицу А-1.
Найдем определитель матрицы А:
D =
Р е ш е н и е. 10. Будем искать обратную матрицу А-1.
Найдем определитель матрицы А:
D = 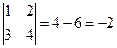 ≠ 0.
Вычислим алгебраические дополнения каждого элемента матрицы А:
А11 = 4; А12 = - 3; А21 = - 2; А22 = 1.
Запишем матрицу ≠ 0.
Вычислим алгебраические дополнения каждого элемента матрицы А:
А11 = 4; А12 = - 3; А21 = - 2; А22 = 1.
Запишем матрицу 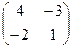 , транспонируем ее: , транспонируем ее: 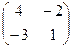 .
Учитывая, что 1/ D = - 1 / 2, запишем обратную матрицу:
А-1 = .
Учитывая, что 1/ D = - 1 / 2, запишем обратную матрицу:
А-1 =  .
20. Умножая матрицу А-1 на матрицу В:
Х = А-1 В = .
20. Умножая матрицу А-1 на матрицу В:
Х = А-1 В = 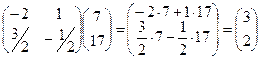 .
30. Так как .
30. Так как  , то по определению равных матриц получим х1 = 3, х2 = 2. , то по определению равных матриц получим х1 = 3, х2 = 2.
|






