относится к той ситуации, когда рассматриваются зависимые случайные величины.
Если имеются зависимые случайные величины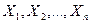 
и если при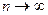 
то среднее арифметическое наблюденных значений случайных величин 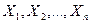сходится по вероятности к среднему арифметическому их математических ожиданий.
Согласно теоремам о числовых характеристиках для зависимых случайных величин
Применяя к величине У неравенство Чебышева и переходя к противоположному событию имеем
,
что и требовалось доказать.
7.4. Следствия закона больших чисел: теоремы Бернулли и Пуассона
Теорема Бернулли утверждает, что при неограниченном увеличении числа опытов n частота события А сходится по вероятности к его вероятности p
,
где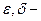 
сколь угодно малые положительные числа.
Большое значение этой теоремы в том, что по статистической вероятности можно с большой долей вероятности оценивать классическую вероятность.
Теорема Пуассона утверждает, что если производится n независимых опытов и вероятность появления события А в i- м опыте равна 
, то при увеличении n частота события А сходится по вероятности к среднему арифметическому вероятностей
.
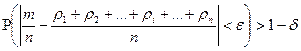8. Центральная предельная теорема для одинаково распределенных случайных величин.
Если 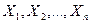, … независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием 
и дисперсией 
, то при неограниченном увеличении n закон распределения суммы 
неограниченно приближается к нормальному закону распределения.
При определенных условиях эта теорема справедлива и для неодинаково распределенных слагаемых.
Например, в качестве таких условий можно привести условия А.М.Ляпунова:
,
где 
третий абсолютный центральный момент величины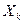 
:
.
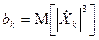Наиболее общим (необходимым и достаточным) условием справедливости центральной предельной теоремы является условие Линдеберга:
при любом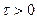 
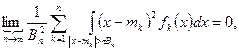
где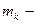 
математическое ожидание, 
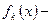плотность распределения случайной величины 
.
