5.1. Математическое ожидание неслучайной величины равно этой величине:
если с – не случайная величина, то 
5.2. Дисперсия не случайной величины равна нулю 
5.3. Вынесение неслучайной величины за знак математического ожидания. Если с – не случайная величина, а Х – случайная, то 
5.4. Вынесение не случайной величины за знак дисперсии: 
Следствие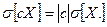 
5.5. Математическое ожидание суммы случайных величин Х иУ равно сумме их математических ожиданий
.
5.6. Дисперсия суммы двух случайных величин равна:
где 
корреляционный момент между Х и У.
Для независимых случайных величин 
.
5.7. Математическое ожидание произведения двух случайных величин равно:
Для независимых случайных величин
5.8. Дисперсия произведения двух независимых случайных величин равна:
.
Следствие: для независимых центрированных случайных величин дисперсия произведения равна произведению дисперсий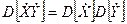 
.
