Математическим ожиданием случайной функции Х(t) называется неслучайная функция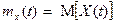 
, которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
Дисперсией случайной функции Х(t) называется неслучайная функция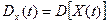 
, значение которой для каждого t равно дисперсии соответствующего сечения случайной функции.
Корреляционной функцией случайной функции Х(t) называется неслучайная функция двух аргументов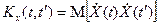 
, которая при каждой паре значений 
равна корреляционному моменту соответствующих сечений случайной функции.
Корреляционная функция имеет большое значение для теории случайных функций, так как дает информацию о наличии линейной связи между значениями случайной функции. Перечислим основные свойства корреляционной функции.
1. При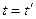 
корреляционная функция обращается в дисперсию случайной функции
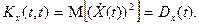
2. От прибавления не случайного слагаемого к случайной функции ее корреляционная функция не меняется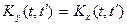 
, где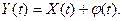 
3. При умножении случайной функции на неслучайную функцию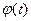 
ее корреляционная функция умножается на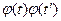 
,
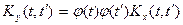где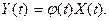 
4. Корреляционная функция центрированной случайной функции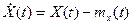 
совпадает с корреляционной функцией случайной функции 
.
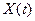Нормированной корреляционной функцией называется функция, определяемая по следующей формуле:
,
которая представляет собой коэффициент корреляции величин для Х(t) и Х(t’).
Взаимной корреляционной функцией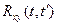 
двух случайных функций Х(t) и У(t) называется функция 
.
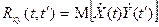Из определения взаимной корреляционной функции вытекает, что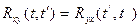 
.
Случайные функции называются некоррелированными, если 
.
Нормированной взаимной корреляционной функцией двух случайных функций Х(t) и У(t) называется функция
.
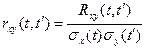Если рассматривается сумма двух случайных функций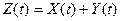 
, то
.
В случае, если случайные функции Х(t) и У(t) не коррелированы, то
.
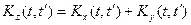