Целью каждого практического занятия является освоение приемов решения конкретных задач для каждого раздела теории вероятностей.
Задачи берутся из сборников задач по теории вероятностей и математической статистики, таких авторов, как А.А.Свешников, Е.С.Вентцель и др., рекомендованных Министерством образования.
При решении задач требуется записать номер решаемой задачи и делать письменную запись текста задачи. Далее фиксируется подробный ход решения задачи с указанием используемых теорем и применяемых законов распределения вероятностей, а также применяемых правил из высшей математики. Ответ сравнивается с ответом,
приводимым в сборниках задач.
1.Непосредственный подсчет вероятностей.
В партии из 
изделий 
бракованных. Определить вероятность того, что среди выбранных наудачу для проверки 
изделий ровно 
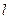окажутся бракованными.
Решение. Число возможных способов взять изделий из равно 
. Благоприятствующими являются случаи, когда из общего числа бракованных изделий взято 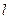(это можно сделать 
способами), а остальные - 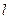изделий не бракованные (это можно сделать 
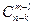способами. Поэтому число благоприятствующих случаев равно 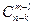. Искомая вероятность равна
.
2. Геометрические вероятности.
В любые моменты промежутка времени 
равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше 
. Определить вероятность того, что приемник будет забит.
Решение. Пусть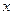 
и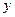 
- моменты поступления сигналов в приемник.
Областью возможных значений 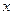, является квадрат площадью 
. Приемник будет забит, если 
. Данная область лежит между прямыми 
и 
. Ее площадь равна 
, поэтому искомая вероятность равна
.
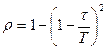3. Теорема умножения вероятностей.
Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4% всей продукции являются браком, а 75% не бракованных изделий удовлетворяют требованиям первого сорта.
Решение. Пусть событие А состоит в том, что выбранное изделие не бракованное, а событие В – выбранное изделие первосортное. Тогда вероятность Р(А) = 1-0,04 = 0,96, а условная вероятность Р(В/А) = 0,75. Искомая вероятность равна вероятности произведения двух событий АВ: 
=Р(АВ) = 0,96×0,75 = 0,72.
4. Теорема сложения вероятностей.
Ведется стрельба по самолету, уязвимыми агрегатами которого являются два двигателя и кабина пилота. Для того, чтобы поразить самолет, достаточно поразить оба двигателя вместе или кабину пилота. Вероятность поражения первого двигателя равна 
, второго двигателя 
, кабины пилота 
. Найти вероятность того, что самолет будет поражен.
Решение. Событие А – поражение самолета есть сумма двух совместных событий: Д – поражение обоих двигателей и К – поражение кабины. Следовательно, Р(А) = Р(Д)+Р(К)-Р(ДК) = + - .
5. Формула полной вероятности.
Прибор может работать в двух режимах: нормальном и не нормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, а не нормальный – в 20%. Вероятность выхода прибора из строя в нормальном режиме равна 0,1, а в не нормальном – 0,7. Найти полную вероятность выхода прибора из строя.
Решение. В соответствии с формулой полной вероятности искомая вероятность равна = 0,8×0,1+0,2×0,7=0,22.
6. Формула Байеса.
В группе из 10 студентов, пришедших на экзамен, 3 отличника, 4 хорошиста, 2 троечника и 1 двоечник. В экзаменационных билетах имеется 20 вопросов. Отличник может ответить на все вопросы, хорошо подготовленный может ответить на 16 вопросов, троечник – на10, двоечник – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент отличник.
Решение. Выдвигаем четыре гипотезы: 
студент отличник; 
студент хорошист; 
студент троечник; 
студент двоечник. До опыта: 
; 
; 
; 
. Событие А – это то, что вызванный студент ответил на три вопроса. Условная вероятность этого события равна
; 
; 
; 
. После опыта, применяя формулу Байеса, имеем:
.
Для сравнения вычислим вероятность, что отвечавший студент был двоечник:
.
