7.1. Неравенство Чебышева.
Пусть имеется случайная величина Х с математическим ожиданием 
и дисперсией 
Неравенство Чебышева утверждает, что, каково бы ни было положительное число α, вероятность того, что величина Х отклонится от своего математического ожидания не меньше чем на α, ограничена сверху величиной 
:
7.2. Закон больших чисел (теорема Чебышева).
Эта теорема устанавливает связь между средним арифметическим наблюденных значений случайной величины и ее математическим ожиданием. Рассмотрим среднее арифметическое значение У для нескольких случайных величин:
Согласно теоремам о числовых характеристиках имеем:
При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию:
где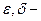 
произвольно малые положительные числа. Доказательство этой теоремы основывается на применении неравенства Чебышева.
Применим к случайной величине У это неравенство, полагая 
: 
.
Как бы мало ни было число 
, можно взять n таким большим, чтобы выполнялось неравенство, 
тогда переходя к противоположному событию, имеем выше приведенное выражение для закона больших чисел.
