Если результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, то имеем дело с системой случайных величин. Условимся систему нескольких случайных величин Х, У,..., W обозначать (Х, У,..., W).
Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих; помимо этого они включают также взаимные связи (зависимости) между случайными величинами.
Законы распределения системы случайных величин.
Функцией распределения системы двух случайных величин (Х, У) называется вероятность совместного выполнения двух неравенств X<x и Y<y:
.
Функция распределения 
обладает следующими свойствами:
1. есть неубывающая функция обоих своих аргументов, т.е.
при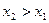 
;
при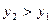 
.
2. Повсюду на - ∞ функция распределения равна нулю:
3. При одном из аргументов, равном + ∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
где 
соответственно функции распределения случайных величин Х и У.
4. Если оба аргумента равны + ∞, функция распределения системы равна единице:
Через функцию распределения легко решается задача вычисления вероятности попадания случайной точки в заданную область, когда эта область представляет собой прямоугольник со сторонами параллельными координатным осям:
Где 
координаты вершин четырех бесконечных квадранта на плоскости х0у.
Плотностью распределения системы двух случайных величин называется функция, которая представляет собой вторую смешанную частную производную функции по х и у, обозначается как 
Для плотности вероятности системы вводится понятие «элемента вероятности», который показывает вероятность попадания случайной точки в элементарный прямоугольник со сторонами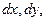 
примыкающий к точке (х,у)
Пользуясь понятием элемента вероятности, легко решается задача вычисления вероятности попадания случайной точки в произвольную область D:
.
Из этой формулы вытекает формула для вероятности попадания в прямоугольник R, ограниченный абсциссами 
и 
и ординатами 
и 
Воспользуемся этой формулой для того, чтобы выразить функцию распределения системы двух случайных величин через плотность распределения:
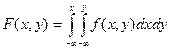
Плотность распределения обладает следующими двумя свойствами:
1. Плотность распределения системы есть функция неотрицательная: 
.
2. Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице:
Законы распределения отдельных случайных величин, входящих в систему. Условные законы распределения.
Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных случайных величин, входящих в систему. Воспользовавшись третьим свойством функции распределения и интегральной связью между функцией распределения и плотностью распределения, напишем
Откуда, дифференцируя по х, получим выражение для плотности распределения величины Х
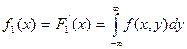
Аналогично
Приведенные формулы дают возможность, зная закон распределения системы, найти законы распределения отдельных величин, входящих в систему. Естественно, возникает вопрос об обратной задаче: нельзя ли по законам распределения отдельных величин, входящих в систему, восстановить закон распределения системы? Оказывается, что в общем случае сделать этого нельзя, так как для этого нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью, так называемых условных законов распределения.
Условным законом распределения величины Х, входящей в систему (Х,У), называется ее закон распределения, вычисленный при условии, что другая случайная величина У приняла определенное значение у. Условная функция распределения обозначается 
условная плотность распределения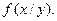 
Зная закон распределения одной из величин, входящих в систему, и условный закон распределения второй, можно составить закон распределения системы. Вывод формулы опирается на использование теоремы умножения вероятностей для зависимых событий:
Эту формулу часто называют теоремой умножения законов распределения. Аналогично можно написать:
Разрешая эти формулы относительно условных законов распределения, получаем:
или
