Случайная величина, значения которой сплошь заполняют некоторый промежуток, называется непрерывной.
В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полубесконечными или бесконечными, например: (a; b ], (–¥; a), [ b; ¥), (–¥;¥).
При описании непрерывной случайной величины принципиально невозможно выписать и занумеровать все её значения, принадлежащие даже достаточно узкому интервалу. Эти значения образуют несчётное множество, называемое «континуум».
Вероятность каждого конкретного значения непрерывной случайной величины равна нулю.
Равную нулю вероятность имеют невозможные события. Оказывается, что и возможные события могут иметь нулевую вероятность.
Это не парадокс. Например, возьмем тело объемом V и массой M. Выделим внутри тела точку А и рассмотрим некоторый объем, включающий эту точку. Начнем стягивать этот объем к точке А: V, V 1, V 2, V 3,... Получим последовательность соответствующих этим объемам уменьшающихся масс: M 1, M 2, M 3, … В пределе при стягивании объема к точке А масса обратится в нуль. То есть, ненулевая масса тела есть сумма бесконечного числа нулевых масс его отдельных точек. Эти затруднения можно обойти, используя понятие плотности.
Пусть x – непрерывная случайная величина. Рассмотрим для некоторого числа х вероятность реализации значений случайной величины в промежутке х < x < х + D х,то есть P (х < x < х + D х). Здесь D х – малый интервал.
Очевидно, что если D х ® 0, то P (х < x < х + D х)® 0. Обозначим f x(х) предел отношения P (х < x < х + D х) к D х при D х ® 0, если такой предел существует:
.
Функция f x(х) называется плотностью распределения вероятностей случайной величины x.
Если такая функция нашлась, можно считать, что случайная величина полностью определена: ведь в этом случае можно вычислить вероятность ее попадания в любой промежуток числовой оси:
Вероятность того, что непрерывная случайная величина принимает значения из отрезка [ a; b ], равна площади под графиком плотности вероятности на этом отрезке.
Плотностью распределения вероятностей может служить любая интегрируемая функция f x(х), удовлетворяющая двум условиям:
1) f x(х)³0 для всех x;
2) 
(условие нормировки).
Пусть x – непрерывная случайная величина. Функция F x(x), которая определяется равенством
,
называется интегральной функцией распределения или просто функцией распределения случайной величины x.
Таким образом, при каждом фиксированном значении аргумента x значение этой функции равно вероятности выполнения неравенства x< x (случайная величина x меньше x). Непосредственно из определения следует равенство
.
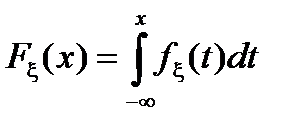Производная определённого интеграла по верхнему пределу приводит к соотношению
.
Плотность распределения f x(x) называют дифференциальной функцией распределения.
Функция распределения F x(x) непрерывной случайной величины x имеет следующие свойства:
1. 0£ F x(x)£1, –¥< x <¥.
2. 
; 
.
3. F x(x) непрерывная неубывающая функция на всей числовой оси.
Свойства 1–3 вытекают непосредственно из определения функции F x(x).
4. Приращение F x(x) на промежутке (х 1; х 2) равно вероятности того, что случайная величина x принимает значение из этого промежутка:
F x(x 2)– F x(x 1)= P (x 1£x< x 2).
Доказательство.
F x(x 2)= P (x< x 2)= P (x< x 1)+ P (x 1£x< x 2)= F x(x 1)+ P (x 1£x< x 2).
Отсюда
P (x 1£x< x 2)= F x(x 2)– F x(x 1), ч.т.д.
Заметим, что для непрерывной случайной величины x справедливы равенства
P (x 1£x< x 2)= P (x 1<x< x 2)= P (x 1<x£ x 2)= P (x 1£x£ x 2),
т.к. вероятность попасть в точку равна нулю: P (x 1)= P (x 2)=0.
Следует отметить, что можно рассматривать функцию распределения не только для непрерывных, но и для дискретных случайных величин. В случае дискретной случайной величины x, функция распределения представляет собой функцию накопленных вероятностей
,
где суммирование распространяется на все значения индекса i, для которых xi < x.
Функция распределения дискретной случайной величины не является непрерывной; она испытывает скачки в тех точках, для которых существует положительная вероятность события {x= x k}. Таким образом,
,
где { xk, k =1,2,3,…} – множество возможных значений случайной величины x.
Свойства 1, 2 и 4 функции распределения F x, рассмотренные для непрерывных случайных величин, остаются в силе и для дискретных величин.
Отметим еще раз, что плотность распределения вероятностей f x(x) может быть введена только для непрерывных величин.
Математическое ожидание непрерывной случайной величины x определяется равенством
. 
Предполагается, что интеграл сходится абсолютно.
Все свойства математического ожидания, указанные выше для дискретных случайных величин, сохраняются и для непрерывных величин.
Если h=j(x) – функция случайного аргумента x, возможные значения которого принадлежат всей оси О х, то
.
Если математическое ожидание М [x] существует и кривая плотности распределения симметрична относительно прямой х = С, то М [x]= С.
Модой Mo непрерывной случайной величины x называют то ее возможное значение, которому соответствует локальный максимум плотности распределения вероятностей. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным.
Медианой Me непрерывной случайной величины x, называют то ее возможное значение, которое определяется равенством
.
Геометрически медиану можно истолковать как точку, в которой ордината f x(x) делит пополам площадь, ограниченную кривой распределения.
Дисперсия непрерывной случайной величины xопределяется равенством
или равносильным равенством
.
Все свойства дисперсии, указанные выше для дискретных случайных величин, сохраняются и для непрерывных величин.
Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины:
Если h=j(x) – функция случайного аргумента, то
Начальный момент порядка k непрерывной случайной величины x определяется равенством
.
Центральный момент порядка k непрерывной случайной величины x определяется равенством
Очевидно, что если k =1, то a1= M [x], m1=0; если k =2, то m2= D [x].
Пример 21. Непрерывная случайная величина Х задана функцией плотности вероятности (дифференциальной функцией распределения) 
Найти функцию распределения F (x) случайной величины Х. Вычислить для Х математическое ожидание M [ X ], дисперсию D [ X ], моду Mo, медиану Me.
Решение. Функцию распределения F (x) непрерывной случайной величины Х найдем по формуле 
.
Если x £0, то f (x)=0, следовательно,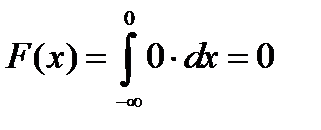 
.
Если 0< x £2, то 
Если x >2, то 
Итак, искомая функция распределения примет вид
Математическое ожидание M [ X ] вычисляем по формуле:
Для нахождения дисперсии D [ X ] воспользуемся формулой
Тогда 
и 
Функция f (x) достигает максимума в точке х =2 (предлагается построить график функции f (x)) и, значит, Мо = 2.
Для нахождения медианы Ме нужно решить уравнение 
(так как медиана делит область значений случайной величины на две равные по вероятности части). Получим 
Случайная величина по условию задачи определена только на интервале 
, значит Ме = 1.414.
